Výzkumná práce "Magnitského aritmetika". Starověké metody řešení problémů při míchání látek z knihy "Aritmetika" od Leontyho Filippoviče Magnitského

GOU SOSH № 000. Moskva

Staré způsoby řešení

míchání úkolů

z knihy "Aritmetika" od Leontyho Filippoviče Magnitského.

PROJEKTOVÁ PRÁCE V MATEMATICE

Vedoucí: učitel matematiky

MOSKVA 2010

1. Úvod ……………………………………………………………………….

2. Leonty Filippovich Magnitskiy je úžasný ruský matematik …… ..3

3. Úkoly pro míchání látek ……………………………………………………………………………… .5

4. Srovnání moderní metodyřešení úloh o míchání látek a Magnitského metodou na příkladech problémů ze života; jednoduchost a srozumitelnost Magnitského metody ………………………………………………………………………………………… 5

5. Použití Magnitského metody v úkolech GIA ………………………………………… 10

6. Literatura ……………………………………………………………………………………………………… ..12

Úvod

V hodinách matematiky, počínaje základní školou, se neustále potýkáme s problémy míchání různých látek. Každým rokem jsou tyto úlohy složitější, ale princip jejich řešení se nemění - jednu část vezmeme jako "x" a vycházíme z ní.

Ale nedávno jsem se dozvěděl, že dříve takové problémy bylo možné vyřešit bez zavádění proměnných, a zajímalo mě to.

Ukazuje se, že takové metody jsou podrobně popsány v knize Leontyho Filippoviče Magnitského. Než vás seznámím s těmito metodami řešení problémů, rád bych vám řekl něco málo o tomto velkém ruském matematikovi.

Leonty Filippovič Magnitsky

Magnitského

Leonty Filippovich, ruský matematik; učitel. Podle některých zpráv studoval na Slovansko-řecko-latinské akademii v Moskvě. Od roku 1701 až do konce svého života vyučoval matematiku na škole matematických a navigačních věd. V roce 1703 vydal svou „Aritmetiku“, která byla až do poloviny 18. století hlavní učebnicí matematiky v Rusku. Díky svým vědeckým, metodologickým a literárním zásluhám byla Magnitského „Aritmetika“ používána i poté, co se objevily další knihy o matematice, více v souladu s novou úrovní vědy. Magnitského kniha byla spíše encyklopedií matematických znalostí než učebnicí aritmetiky, mnohé z informací v ní obsažených byly poprvé uvedeny v ruské literatuře. "Aritmetika" hrála důležitou roli v šíření matematických znalostí v Rusku; z ní studoval, který tuto učebnici nazval „bránami učení“.

Rýže. 1. Leonty Filippovič Magnitskij () je úžasný ruský matematik.

Míchání úkolů

S takovými úkoly se v životě setkáváme často – v hutnictví, chemické výrobě, v medicíně a farmakologii a dokonce i v běžném životě, například při vaření.

V metalurgii takové problémy vznikají, když potřebujete znát složení různých slitin, v chemii - množství látky, která reaguje, v medicíně a farmakologii výsledek léčby často závisí na dávce léčivé látky a jejích složek, a při vaření - chuť výsledného pokrmu.

Obvykle potřebujeme zjistit, jak ze dvou roztoků získat látku o požadované koncentraci, co a v jakém množství přidat, jaký je podíl každé ze složek.

Jak nyní řešíme takové problémy?

Jednu část vezmeme jako "X", poskládáme rovnice, případně zavedeme druhou proměnnou, vyřešíme a získáme požadované hodnoty.

na počátku 18. století, kdy použití proměnných ještě nebylo akceptováno, navrhl důmyslnou grafickou metodu řešení takových problémů.

Srovnání moderních metod řešení úloh o míchání látek a Magnitského metody na příkladech problémů ze života; jednoduchost a jasnost Magnitského metody.

Zvažte Magnitského metodu, kterou jsme podmíněně nazvali „ryba“ na příkladu problému míchání olejů.

Jak míchat oleje?

Jistá osoba měla tučné oleje. Jeden - za cenu deseti hřiven za kbelík a druhý - šest hřiven za kbelík.

Chtěl z těchto dvou olejů smícháním vyrobit máslo za cenu sedmi hřiven za kbelík.

Otázka: v jakém poměru by měly být tyto dva oleje smíchány?

Moderní způsob řešení problému.

Vezměme si jeden díl levné ropy za „X“. A část drahé ropy - pro "Y" a dostaneme následující rovnici:

7 (x + y) = 6x + 10y

Dostali jsme, že oleje je třeba smíchat v poměru 1 ku 3

Starý způsob řešení problému.

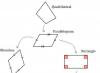
Zde je způsob, jak tento problém vyřešit (obr. 2).

Do středu napíšeme cenu prvního oleje - 6. Pod ním, sestupem dolů, zapíšeme cenu druhého oleje. Vlevo, přibližně uprostřed mezi horním a dolním číslem, napíšeme cenu požadovaného oleje. Spojujeme tři čísla úsečkami. Dostaneme obrázek obr. 2-a.

Od ceny smíšené ropy odečteme první cenu, protože je nižší než cena požadované ropy, a výsledek dáme vpravo od druhé ceny diagonálně vzhledem k první ceně. Poté od druhé ceny, která je více než cena požadovaného oleje, odečteme cenu smíšeného oleje a to, co zbylo, zapíšeme vpravo od první ceny diagonálně k druhé ceně. Spojíme body úsečkami a dostaneme následující obrázek - Obr. 2-b.

Poté určíme poměr hodnot získaných vpravo k sobě navzájem. Vidíme, že vedle ceny levné ropy je číslo 3 a vedle ceny drahé ropy je číslo 1. To znamená

že levná ropa by se měla brát třikrát více než drahá, to znamená, že chcete-li získat ropu za cenu 7 hřiven, musíte vzít ropu v poměru 1 ku 3, to znamená, že levná ropa by měla být třikrát více než drahý olej.

Porovnáním obou metod - moderní a staré (Magnitsky), vidíme, že odpovědi získané těmito dvěma metodami jsou totožné, což znamená, že tato metoda je docela použitelná pro řešení tohoto problému míchání látek.

Zvažme další podobné úkoly.

Úkol míchání látek v každodenním životě.

Může být tato technika užitečná v moderním životě? Samozřejmě může např. v kadeřnickém salonu.

Jednou za mnou v kadeřnickém salonu přišel mistr s nečekanou prosbou:

- Pomůžete nám vyřešit problém, se kterým si nevíme rady?

- Kolik řešení bylo kvůli tomu zkaženo! - přidal další mistr.

- Jaký je úkol? Zeptal jsem se.

- Máme dva roztoky peroxidu vodíku: 30% a 3%. Musíte získat 12% roztok. Můžete nám pomoci správně vypočítat proporce?

Jak tento problém vyřešíme?

Zde jsou dva způsoby, jak problém vyřešit.

Označme požadovanou část 30% roztoku - x a 3% - řešení - y. V souladu s tím musíte získat 0,12 (x + y).

Napíšeme rovnici:

0,03y + 0,3x = 0,12 (x + y)

0,3x-0,12x = 0,12y-0,03y

Odpověď: Chcete-li získat 12% roztok, musíte vzít jeden díl 30% roztoku a dva díly 3% roztoku peroxidu.

Druhou metodou je Magnitského metoda.

Do středu napíšeme koncentraci prvního roztoku – 30 %. Pod něj, směrem dolů, zapíšeme koncentraci druhého roztoku - 3% nebo 0,03. Vlevo, přibližně uprostřed mezi horním a dolním číslem, zapíšeme koncentraci požadovaného roztoku - 12% nebo 0,2. spojte tři čísla rovnými čarami.

Od první koncentrace, protože je větší než požadovaná, odečtěte 0,12 a podepište výsledek 0, 18 vpravo od 0,03, což se ukázalo být diagonálně od 0,3. Od 0, 12 odečteme 0, 03 a výsledek podepíšeme vpravo od 0,3 - 0,09, což také vyjde diagonálně od hodnoty 0, 03. Vše spojíme segmenty a získáme „rybu“ (obr. 3 ).

Poměr získaných hodnot - 0, 09 a 0,018 - je 1 ku 2, to znamená, že první roztok s koncentrací 30% by měl být užíván 2krát méně než 3% roztok.

Odpovědi získané těmito dvěma metodami jsou totožné.

Jak vidíte, řešení bez zadávání proměnných je mnohem jednodušší a přehlednější.

Využití Magnitského metody v úkolech GIA.

Dříve nebo později budeme muset všichni složit zkoušky v podobě Jednotné státní zkoušky nebo Státní zkušební agentury. Právě v GIA je úkol smíchat látky v části C.

To je úkol sám.

Existují dvě slitiny s různým obsahem zlata. V první slitině - 35% zlata a ve druhé 60%, v jakém poměru by se měla vzít první a druhá slitina, aby se z nich získala nová, obsahující 40% zlata.

Tento problém vyřešíme dvěma způsoby.

Nechť část první slitiny je x a druhá - y

Potom je množství zlata v první slitině 0,35x a ve druhé 0,6y. Hmotnost nové slitiny je x + y a množství zlata je 0,4 (x + y).

Udělejme rovnici:

0,35x + 0,6y = 0,4 (x + y)

35x + 60y = 40x + 40y

Odpověď: pro získání slitiny obsahující 40 % zlata ze dvou slitin s obsahem 35 % a 60 % je třeba vzít 4x více 35 % slitiny.

Metoda 2 - Magnitského metoda.

Podobně jako u výše popsané metody ryb vytvoříme obrázek znázorněný na obrázku 4.

Výsledek: poměr získaných hodnot je 1 ku 4, což znamená, že 35% slitiny by mělo být 4krát více než 60%.

Jak opět vidíte, metoda Leontyho Filippoviče Magnitského je srozumitelnější.

Použití této metody vám může pomoci rychle a správně vyřešit tento poměrně obtížný problém a také, kdo ví, možná dostanete další body za neobvyklé řešení!

Uvedené příklady ukazují, že elegantní grafická metoda řešení problémů míchání látek dnes neztratila na aktuálnosti a atraktivitě. Úspěchy moderní matematiky v žádném případě nesnižují zásluhy pozoruhodných ruských vědců, kteří pracovali před několika staletími, na něž by ti, kdo studují matematiku, neměli zapomínat ani dnes.

Literatura:

1., . Starověké zábavné úkoly. Moskva, „Nauka“, hlavní redakce fyziky a matematiky, 1985.

2. // Encyklopedický slovník Brockhause a Efrona: V 86 svazcích (82 svazcích a 4 dodatečné). - SPb.: 1890-1907.

3. P. Postavy ruských dějin. Životopisná referenční kniha. Moskva, 1997

4.http: // ru. wikipedie. org / wiki /% D0% 9C% D0% B0% D0% B3% D0% BD% D0% B8% D1% 86% D0% BA% D0% B8% D0% B9_% D0% 9B.

Zpět dopředu

Pozornost! Náhledy snímků mají pouze informativní charakter a nemusí představovat všechny možnosti prezentace. Pokud vás tato práce zaujala, stáhněte si prosím plnou verzi.

Matematika, která se odedávna stala jazykem vědy a techniky, nyní stále více proniká do každodenního života a každodenního jazyka a stále více se zavádí do oblastí, které jsou jí tradičně vzdálené.

Hlavním úkolem výuky matematiky ve škole je zajistit studentům solidní a vědomé zvládnutí systému matematických znalostí a dovedností nezbytných v každodenním životě a pracovních činnostech každého člena moderní společnosti, postačujících ke studiu příbuzných oborů a dalšímu vzdělávání, jako stejně tak odborná činnost vyžadující dostatečně vysokou matematickou kulturu. Pro život v moderní společnost důležité je vytvoření matematického stylu myšlení, projevujícího se v určitých mentálních dovednostech.

Téma „Zájem“ je univerzální v tom smyslu, že propojuje mnoho exaktních a přírodních věd, domácnosti a průmyslové sféry života. Studenti se setkávají s procenty ve fyzice, chemii, čtení novin, sledování televize. Ne všichni studenti mají schopnost kvalifikovaně a ekonomicky provádět elementární procentuální výpočty. Praxe ukazuje, že velmi mnoho absolventů středních škol nejenže nemá silné dovednosti v zacházení se zájmem v běžném životě, ale nechápe ani význam zájmu jako zlomku dané hodnoty. Děje se tak proto, že procenta se studují na prvním stupni základní školy, v 5.–6. ročníku, kdy si žáci z důvodu věkových charakteristik ještě nemohou udělat plnohodnotnou představu o procentech a jejich roli v běžném životě.

Nově jsou v kontrolních a měřících materiálech zkoušky z matematiky, konané formou zkoušky, zařazeny úlohy na procenta, směsi a slitiny.

ÚKOLY Z VARIANT POUŽITÍ

7 litrů vody bylo přidáno do nádoby obsahující 5 litrů 12% vodného roztoku nějaké látky. Kolik procent je koncentrace výsledného roztoku?
Určité množství 15% roztoku určité látky bylo smícháno se stejným množstvím 19% roztoku této látky. Kolik procent je koncentrace výsledného roztoku?
Smíchané 4 litry 15% vodného roztoku nějaké látky se 6 litry 25% vodného roztoku stejné látky. Kolik procent je koncentrace výsledného roztoku?
K dispozici jsou dvě slitiny. První obsahuje 10 % niklu, druhý 30 % niklu. Z těchto dvou slitin byla získána třetí slitina o hmotnosti 200 kg obsahující 25 % niklu. O kolik kilogramů je hmotnost první slitiny menší než hmotnost druhé?
První slitina obsahuje 10 % mědi, druhá 40 % mědi. Hmotnost druhé slitiny je o 3 kg větší než hmotnost první slitiny. Z těchto dvou slitin byla získána třetí slitina obsahující 30 % mědi. Najděte hmotnost třetí slitiny. Svou odpověď uveďte v kilogramech.
Smícháním 30% a 60% roztoků kyseliny a přidáním 10 kg čisté vody byl získán 36% roztok kyseliny. Pokud by se místo 10 kg vody přidalo 10 kg 50% roztoku stejné kyseliny, pak by se získal 41% roztok kyseliny. Kolik kilogramů 30% roztoku bylo použito k výrobě směsi?
Jsou zde dvě plavidla. První obsahuje 30 kg a druhý - 20 kg kyselého roztoku různých koncentrací. Pokud se tyto roztoky smíchají, získáte roztok obsahující 68% kyseliny. Pokud smícháte stejné množství těchto roztoků, získáte roztok obsahující 70% kyseliny. Kolik kilogramů kyseliny je v první nádobě?

ÚKOLY Z PŘIJÍMACÍCH ZKOUŠEK NA MSU

MATEMATICKÁ FAKULTA. Jsou tam tři kovové ingoty. První váží 5 kg, druhý 3 kg a každý z těchto dvou slitků obsahuje 30 % mědi. Je-li první ingot tavený se třetím, získáte ingot obsahující 56 % mědi, a pokud je druhý ingot tavený s třetím, získáte ingot obsahující 60 % mědi. Najděte hmotnost třetího ingotu a procento mědi v něm.

CHEMICKÁ FAKULTA. Nádoba o objemu 8 litrů je naplněna směsí kyslíku a dusíku. Kyslík tvoří 16 % kapacity plavidla. Z nádoby se uvolní určité množství směsi a vstříkne se stejné množství dusíku, načež se opět uvolní stejné množství směsi jako poprvé a znovu se přidá stejné množství dusíku. Nová směs obsahovala 9 % kyslíku. Kolik směsi bylo pokaždé vypuštěno z nádoby?

EKONOMICKÁ FAKULTA. Banka plánuje investovat na 1 rok 40 % prostředků svých klientů do projektu X a zbývajících 60 % do projektu Y. Projekt X může podle okolností přinést zisk ve výši 19 až 24 % ročně, a projekt Y - od 29 do 34 % ročně. Na konci roku je banka povinna vrátit peníze zákazníkům a vyplatit jim úrok v předem stanovené sazbě. Určete nejnižší a nejvyšší možnou úroveň úrokové sazby z vkladů, při které bude čistý zisk banky činit minimálně 10 a maximálně 15 % ročně z celkových investic do projektů X a Y.

SOCIOLOGICKÁ FAKULTA. Průzkum byl proveden v předškolním zařízení. Na otázku: "Co máš radši kaši nebo kompot?" - většina odpověděla: „Kashu“, menší: „Kompot“ a jeden respondent: „Je pro mě těžké odpovědět“. Dále bylo zjištěno, že mezi milovníky kompotu preferuje 30 % meruňky a 70 % hrušky. Milovníci kaší dostali otázku, jakou kaši preferují. Ukázalo se, že 56,25 % zvolilo krupicovou kaši, 37,5 % rýžovou a pouze jeden odpověděl: "Těžko odpovědět." Kolik dětí bylo dotazováno?

V tomto ohledu vyvstalo nutné posílit praktickou orientaci výuky, zařadit do práce se studenty odpovídající úlohy na procenta, proporce, grafy reálných závislostí, slovní úlohy s konstrukcí matematických modelů reálných situací. V procesu přípravy je třeba hledat různé způsoby řešení takových typů úkolů, jako jsou úkoly „na pohyb“, „na práci“, „procenta“, „směsi a slitiny“ ...

Téma „Zájem“ je vlastně poměrně rozsáhlé a dnes bych se rád zastavil u jedné z jeho sekcí – problémy o směsích a slitinách, tím spíše, že při řešení úloh o směsích a slitinách jsou zřejmé mezioborové souvislosti s chemií, fyzikou a ekonomií, znalosti tím se zvyšuje vzdělávací motivace studentů ve všech předmětech.

Pokud je totiž člověk nadaný v jedné věci, většinou je talentovaný v mnoha ohledech.

Nejprve je ale nutné připomenout některé teoretické základy řešení problémů se směsmi a slitinami (Snímek 5).

V procesu hledání řešení těchto problémů je užitečné použít velmi pohodlný model a naučit ho používat školáky. Každou směs (slitinu) zobrazujeme ve formě obdélníku rozděleného na fragmenty, jejichž počet odpovídá počtu prvků tvořících tuto směs (tuto slitinu).

Zvažte následující problém jako příklad.

Problém 1. Existují dvě slitiny mědi a cínu. Jedna slitina obsahuje 72 % mědi a druhá 80 % mědi. Kolik z každé slitiny byste měli vzít, abyste vyrobili 800 g slitiny obsahující 75 % mědi?

Znázorněme každou ze slitin ve formě obdélníku, rozděleného na dva fragmenty podle počtu vstupujících prvků. Model navíc zobrazí charakter operace – fúzi. Za tímto účelem mezi první a druhý obdélník vložíme znaménko „+“ a mezi druhý a třetí obdélník vložíme znaménko „=“. To ukazuje, že třetí slitina se získá tavením prvních dvou. Výsledný obvod je následující:

Nyní vyplňte výsledné obdélníky podle stavu problému.

Nad každým obdélníkem uvedeme odpovídající složky slitiny. V tomto případě obvykle postačí použít první písmena jejich jména (pokud se liší). Je vhodné zachovat pořadí odpovídajících písmen.

Do obdélníků napište procento (nebo část) odpovídající složky. Pokud se slitina skládá ze dvou složek, pak stačí uvést procento jedné z nich. V tomto případě se procento druhého rovná rozdílu mezi 100 % a procentem prvního.

Pod obdélník zapíšeme hmotnost (nebo objem) příslušné slitiny (nebo součásti).

Proces uvažovaný v problému může být reprezentován jako následující modelové schéma:

Řešení.

1. způsob. Nech být NS G Je hmotnost první slitiny. Poté (800 - NS ) g je hmotnost druhé slitiny. Doplňme poslední schéma těmito výrazy. Dostaneme následující schéma:

Součet hmotností mědi v prvních dvou slitinách (tj. nalevo od rovnítka) se rovná hmotnosti mědi ve výsledné třetí slitině (napravo od rovnítka):.

Po vyřešení této rovnice dostaneme hodnotu At NS výraz . To znamená, že první slitina musí být odebrána 500 g a druhá - 300 g.

Odpověď: 500 g, 300 g.

2. způsob. Nech být NS r a na g je hmotnost první a druhé slitiny, to znamená, nechť má původní schéma tvar:

Každá z rovnic systému dvou lineárních rovnic ve dvou proměnných se snadno stanoví:

Řešení systému vede k výsledku: To znamená, že první slitina by měla být odebrána 500 g a druhá - 300 g.

Odpověď: 500 g, 300 g.

Uvažovaný model usnadňuje studentům přechod od podmínky problému k jeho přímé realizaci standardními způsoby: ve formě rovnic nebo soustav rovnic.

Zvláště zajímavé jsou dvě další metody, které redukují řešení těchto problémů na triviální verzi založenou na aritmetice a konceptu proporcí.

Starý způsob řešení

Tímto způsobem můžete řešit problémy míchání (fúze) libovolného počtu látek. Problémům tohoto typu byla věnována značná pozornost ve starých rukopisech a "Aritmetice" od Leontyho Filippoviče Magnitského (1703). (Leontij Filippovič Magnitskij (při narození Teljatin; 9. (19.) června 1669, Ostaškov - 19. (30. října), 1739, Moskva) - ruský matematik, učitel. Učitel matematiky na Škole matematických a navigačních věd v Moskvě (od r. 1701 až 1739), autor první vzdělávací encyklopedie v matematice v Rusku).

Tato metoda umožňuje získat správnou odpověď ve velmi krátkém čase a s minimálním úsilím.

Vyřešíme předchozí úkol 1 starým způsobem.

Pod sebou je napsáno procento mědi v dostupných slitinách, vlevo od nich a přibližně uprostřed - procento mědi ve slitině, které by mělo být získáno po legování. Spojením zapsaných čísel s pomlčkami získáme následující schéma:

Uvažujme dvojice 75 a 72; 75 a 80. V každém páru více odečtěte menší a napište výsledek na konec odpovídající šipky. Získáte následující schéma:

Z toho se usuzuje, že 72% slitiny by mělo být vzato 5 dílů a 80% - 3 díly (800: (5 + 3) = 100 g připadá na jeden díl.) K získání 800 g 75% -té slitiny , musíte vzít 72% slitinu 100 5 = 500 g a 80% - 100 3 = 300 g.

Odpověď: 500 g, 300 g.

Úkol 2 . V jakém poměru je potřeba slitiny 375 zlata se 750 zlatem získat 500 zlata?

Odpověď: Musíte vzít dvě části 375. vzorku a jednu část 750. vzorku.

Křížové pravidlo nebo Pearsonův čtverec

(Karl (Charles) Pearson (27. března 1857, Londýn – 27. dubna 1936, tamtéž) – vynikající anglický matematik, statistik, biolog a filozof; zakladatel matematické statistiky, autor více než 650 publikovaných vědeckých prací.

Velmi často se při řešení úloh musíme setkat s případy přípravy roztoků s určitým hmotnostním zlomkem rozpuštěné látky, smícháním dvou roztoků různých koncentrací nebo ředěním silného roztoku vodou. V některých případech lze provést poměrně složitý aritmetický výpočet. To je však neproduktivní. Častěji je proto lepší použít pravidlo míchání (diagonální model "Pearsonova čtverce" nebo, což je totéž, pravidlo kříže).

Řekněme, že potřebujete připravit roztok o určité koncentraci, přičemž máte k dispozici dva roztoky s vyšší a nižší koncentrací, než potřebujeme. Pokud tedy označíme hmotnost prvního roztoku přes m 1 a druhého přes m 2, pak při míchání bude celková hmotnost směsi součtem těchto hmotností. Nechť hmotnostní zlomek rozpuštěné látky v prvním roztoku -

Při řešení úloh pro roztoky s různou koncentrací se nejčastěji používá diagonální schéma mísícího pravidla. Při počítání zapisujte jeden nad druhý hmotnostní zlomky rozpuštěné látky v původních roztocích, vpravo mezi nimi - její hmotnostní zlomek v připravovaném roztoku a odečíst diagonálně od větší k menší hodnotě. Rozdíly mezi jejich odečtením ukazují hmotnostní zlomky pro první a druhý roztok potřebné k přípravě požadovaného roztoku.

ω 1 , ω 2 - hmotnostní díly prvního a druhého řešení.

Abychom toto pravidlo objasnili, vyřešme nejprve nejjednodušší problém.

Problém 3 . Mořská voda obsahuje 5 % soli (hmotnostní). Kolik čerstvou vodu nutno přidat do 30 kg mořské vody tak, aby koncentrace soli byla 1,5 %?

Odpovědět: 7 kilogramů.

Touto metodou lze také řešit problémy se směsmi a slitinami. Část roztoku se nalila, kousek slitiny se odřízl. Během této operace zůstává koncentrace látek nezměněna.

Na závěr rozhovoru o řešení problémů pro směsi a slitiny poznamenávám, že s vnějším rozdílem v grafu jsou problémy pro slitiny, směsi, koncentrace, pro sloučeninu nebo pro separaci různých látek řešeny podle obecného schématu. (Viz příklady řešení problémů v Prezentaci).

Tím pádem, práce navíc pro rozvoj a zdokonalování dovednosti řešit problémy procentem je významná nejen pro budoucí uchazeče, kteří se s takovými úkoly mohou u zkoušky setkat, ale také pro všechny studenty, neboť moderní život nevyhnutelně vás přiměje řešit problémy se zájmem ve vašem každodenním životě.

Život je ozdoben dvěma věcmi: dělat matematiku a učit ji!
S. Poisson

Borzenková Angela, Surkov Michail, Sokolov Andrey

Autoři, žáci ročníku 7B, SOSH 134, Petrohrad pod vedením učitelky matematiky A.E. Nechaeva. prováděl výzkumné práce na téma "Magnitského aritmetika". Prezenční obhajoba výzkumu proběhla 15. 4. 17 na IV. vědecko-praktické konferenci studentů Krasnogvardejského okresu Petrohradu "WORLD OF SCIENCE" (bez publikace). Tímto jednáním je provedeno zveřejnění díla v hromadných sdělovacích prostředcích.

Stažení:

Náhled:

Chcete-li použít náhled, vytvořte si účet Google (účet) a přihlaste se do něj: https://accounts.google.com

Náhled:

Chcete-li použít náhled prezentací, vytvořte si účet Google (účet) a přihlaste se do něj: https://accounts.google.com

Popisky snímků:

ARITHMETIKA MAGNITSKY Relevance Relevantnost zvoleného tématu je dána: příležitostí seznámit se s první ruskou učebnicí matematiky, historií jejího vzniku, identifikovat historický význam jejího vzhledu a vlivu na rozvoj matematické vědy v Rusko.

Magnitského hypotéza Aritmetiky, která se stala první ruskou učebnicí matematiky, přispěla k: vytvoření jednotného přístupu ke studiu matematiky v Rusku; zvýšení počtu studentů studujících základy matematiky v Rusku díky tomu, že byla psána v ruštině a stala se hlavní učebnicí matematiky v nově vytvořené Navigační škole; a stal se také historickým dokladem některých aspektů života ruských občanů na počátku 18. století.

ARITMETIKA MAGNISKÉHO PROBLÉMU a METODY výzkumu Cíle výzkumu. Dělat krátká recenze retrospektivy vzniku aritmetiky, biografie Leontyho Filippoviče Magnitského, seznámí s historií vzniku aritmetiky a odhalí míru vlivu aritmetiky na šíření matematiky v Rusku. Metody výzkumu. Jako výzkumné metody jsme použili takové obecné vědecké metody, jako je empirická metoda, metoda srovnávání, zobecňování.

Magnitského aritmetika hlavní obsah Historická retrospektiva vzniku Magnitského aritmetiky O Leonty Filippoviči Magnitském O učebnici Magnitského aritmetika Závěr

Aritmetika Magnitského Historická retrospektiva vzniku aritmetiky Magnitského severní války v letech 1700-1721. - je vyžadováno mnoho kvalifikovaných odborníků Učebnic bylo málo. V ruštině nebyly žádné učebnice. Existovaly učebnice v latině, řečtině, uchovávané v "uzavřených" knihovnách, například biskupské školy, vzácné rukopisy Sucharevova věž - budova plavební školy, vytvořená v roce 1701

ARITHMETIKA MAGNITSKY O Leontym Filippoviči Magnitském Dne 9. června 1669 se podle starého stylu narodil budoucí matematik Leonty v rodině rolníka Filipa, přezdívaného Teljašin z patriarchální osady Ostaškov v provincii Tver. V roce 1684, ve věku 14 let, byl Leonty poslán do kláštera Joseph-Volokolamsk. O rok později požehnal opat Leontymu ke studiu na Slovansko-řecko-latinské akademii, která byla v těch letech hlavní vzdělávací institucí v Rusku, ve které studoval asi osm let. V roce 1700 Petr I. nařídil, aby se Leonty jmenoval Leonty Filippovič Magnitsky. V roce 1701 se pak Magnitskij stává státním úředníkem, kterému car Petr I. klade za úkol vytvořit první ruskojazyčnou učebnici matematiky. Od téhož roku až do roku 1739 život L.F. Magnitskij je nerozlučně spjat s činností Navigační školy, kterou v roce 1701 otevřel Petr I. V roce 1739, ve věku 70 let, L.F. Magnitsky zemřel.

ARITHMETIKA MAGNISKIHO O učebnici aritmetiky Magnitského Petra Objednal jsem L.F. Magnitského napsat učebnici matematiky pro plavební školu založenou 14. ledna 1701 v ruštině

ARITHMETIKA MAGNITSKY O učebnici aritmetiky Magnitského

ARITMETIKA MAGNITSKÉHO studijní průvodce v matematice tím, že zavádí pohodlné, podobné arabskému, číslování, zapisuje pokročilé algoritmy té doby sčítání, odčítání, násobení, dělení. Prezentace materiálu je založena na řešení praktických problémů, což umožňuje využívat učebnici k sebevzdělávání. Vědecká novinka. V každé časové fázi je srovnání moderních vzdělávacích metod, algoritmů pro řešení matematických problémů s těmi, které uvádí Magnitského aritmetika, z vědeckého hlediska oprávněné, protože umožňuje posoudit úroveň evoluce matematického vědeckého myšlení, úroveň vývoj všeobecného vzdělání.

Aritmetika Magnitského zdroje Aritmetika Magnitského. Přesná reprodukce originálu. S přílohou článku P. Baranova. - M .: Publishing P. Baranov, 1914. URL: http://elibrary.orenlib.ru/index.php?dn=down&to=open&id=1261 Belenchuk L.N., Osvícení v době Petra Velikého // Domácí i zahraniční pedagogika. I. Institut strategie rozvoje vzdělávání Ruská akademie vzdělávání. - 2016. - č. 3 (30). - S. 54-68. URL: http://elibrary.ru/download/elibrary_26286817_93418862.pdf Denisov A.P., Leonty Filippovich Magnitsky (1669–1739) // M .: Vzdělávání. - 1967 .-- 143 s. Magnitsky Leonty Filippovich // Brockhaus a Efron Encyklopedický slovník: V 86 svazcích (82 svazcích a 4 dodatečné), Petrohrad: 1890-1907. Malykh A.E., Danilova V.I., Leonty Filippovich Magnitsky (1669–1739) // Bulletin Permské univerzity, matematika. Mechanika. Počítačová věda. - 2010. - Vydání. 4 (4). - S. 84-94. URL: http://elibrary.ru/download/elibrary_15624452_71219613.pdf Stepanenko G.A., Magnitského učebnice aritmetiky a moderní matematiky pro základní školy // Tavrichesky Scientific Observer, I. Společnost s ručením omezeným "Meziregionální institut pro rozvoj území Yalta" - 2016. - 1-3 (6) - S. 38-43. URL: http://elibrary.ru/download/elibrary_25473094_94425485.pdf Tikhonova O. Yu. Leonty Filippovich Magnitsky - matematik a křesťan // Vědecko-metodický elektronický časopis "Concept". - 2016. - č. 3 (březen). - S. 71–75. - URL: http://e-koncept.ru/2016/16053.htm Chekin A.L., Borisova E.V., První ruská tištěná učebnice „Aritmetika“ od L.F. Magnitsky // Deník “ Základní škola", I. Společnost s ručením omezeným" Základní škola a školství "Nakladatelství, Moskva. - 2013. - č. 9. - str. 12-15. URL: http://elibrary.ru/download/elibrary_21131169_20173013.pdf 9.http: //museum.lomic.ru/trip.html - webové stránky M.V. Lomonosov ve vesnici Lomonosovo,

ARITMETICKÉ MAGNITSKY zdroje DĚKUJI ZA POZORNOST

Usanova Yana

Výzkumná práce "Řešení problémů z Magnitského aritmetiky". Dílo vypráví o životě a díle Leontyho Filippoviče Magnitského. Uvažuje se o řešení problému „Kadi pitya“ (4 způsoby) a problému „trojitého pravidla“.

Stažení:

Náhled:

Městský vzdělávací ústav

střední škola číslo 2 města Kuzněck

__________________________________________________________________

Řešení problému z Magnitsky Arithmetic

Výzkumná práce

Zpracovala žákyně 6. třídy

Usanova Y.

Vedoucí: O. V. Morozová -

Učitel matematiky

Kuzněck, 2015

Úvod ………………………………………………………………………………………… .3

1. Životopis L.F. Magnitský ………………………………………………… .4

2. Magnitského aritmetika ………………………………………………………… .7

3. Řešení úlohy "Kadi pitya" z Magnitského aritmetiky. Úkoly pro „Trojité pravidlo“ ………………………………………………………… .. 11

Závěr ……………………………………………………………………… 15

Reference …………………………………………………………………… .16

Úvod

Relevance a výběrTémata mé výzkumné práce jsou určena následujícími faktory:

Před vydáním knihy LF Magnitského „Aritmetika“ v Rusku neexistovala žádná tištěná učebnice pro výuku matematiky;

LF Magnitskiy nejen systematizoval stávající znalosti v matematice, ale také sestavil mnoho tabulek, zavedl nová označení.

Cílová:

- Studium dějin matematiky a řešení problémů z knihy L.F. Magnitského.

úkoly:

Prostudujte si životopis L.F. Magnitsky a jeho přínos k rozvoji matematického vzdělávání v Rusku;

Zvažte obsah jeho učebnice;

Vyřešte problém „Kadi pitya“ různými způsoby;

Hypotéza:

Pokud si prostuduji životopis L.F. Magnitského a způsoby řešení problémů, mohu studentům naší školy přiblížit roli matematiky v moderní společnosti. Bude to zábava a zvýší to váš zájem o učení matematiky.

Metody výzkumu:

Studium literatury, informace nalezené na internetu, rozbory, navazování vazeb mezi řešením podle L. F. Magnitského a moderními metodami řešení matematických problémů.

Životopis L.F. Magnitského

19. června 1669, od té doby uplynula 3 století, se ve městě Ostaškov, na území, kde začíná velká ruská řeka Volha, narodil chlapec. Narodil se v malém dřevěný dům, který se nachází u zdí Znamenského kláštera, na břehu jezera Seliger. Narodil se do velké rolnické rodiny Telyashinů, proslulé svou religiozitou. Narodil se v době, kdy na Seligerské zemi vzkvétal klášter Nilova Pustyn. Při křtu dostalo dítě jméno Leonty, což v řečtině znamená „lev“.

Jak šel čas. Chlapec rostl a sílil na duchu. Pomáhal svému otci, který „prácí svých rukou živil sebe“ a svou rodinu, a v volný čas"Byl tam vášnivý lovec, který v kostele četl složité a obtížné." Běžné selské děti neměly možnost mít knihy ani se naučit číst a psát. A mládež Leonty takovou příležitost měla. Jeho prastrýc, Saint Nektarios, byl druhým opatem a stavitelem Nilo-Stolobenské Ermitáže, která vznikla na místě hrdinských činů velkého ruského Svatého Nilu. Dva roky před narozením Leontyho byly nalezeny ostatky tohoto světce a mnoho lidí začalo spěchat na pouť na ostrov Stolbny, kde se nachází poušť. Na toto zázračné místo se vydala i rodina Teljashinů. A při návštěvě kláštera se Leonty dlouho zdržel v klášterní knihovně. Četl staré ručně psané knihy, nevnímal čas, čtení ho pohlcovalo.

Jezero Seliger je bohaté na ryby. Jakmile byla vytvořena sáňkařská trasa, byly konvoje se zmrazenými rybami poslány do Moskvy, Tveru a dalších měst. S tímto vozovým vlakem byl vyslán mladý muž Leonty. Bylo mu tehdy asi šestnáct let.

V klášteře žasli nad neobvyklými schopnostmi obyčejného selského syna: uměl číst a psát, což obyčejní rolníci většinou neuměli. Mniši se rozhodli, že se tento mladý muž stane dobrým čtenářem, a nechali si to „ke čtení“. Poté byl Teljašin poslán do moskevského Simonovova kláštera. Mladík tam všechny ohromil svými mimořádnými schopnostmi. Opat kláštera rozhodl, že takový nuget je třeba dále studovat a poslal ho studovat na Slovansko-řecko-latinskou akademii. Zvláštního zájmu mladý muž vyvolané matematické úkoly. A protože se v té době na akademii nevyučovala matematika a ruských matematických rukopisů bylo omezené množství, studoval tento předmět slovy svého syna Ivana „podivuhodným a neuvěřitelným způsobem“. K tomu se sám učil latinu, řečtinu na akademii, němčinu, holandštinu, italštinu. Po studiích jazyků znovu přečetl mnoho cizích rukopisů a ovládl matematiku natolik, že ho začali zvát do bohatých rodin, aby vyučoval tento předmět.

Leonty Filippovich při návštěvě svých studentů čelil problému. V matematice, nebo jak se říkalo počtům, neexistovala jediná příručka a jediná učebnice pro děti a mládež. Mladík si sám začal skládat příklady a zajímavé problémy. Své téma vysvětloval s takovou vervou, že dokázal zaujmout i toho nejlínějšího studenta, který se nechtěl učit, jakých bylo v bohatých rodinách mnoho.

Zvěsti o talentovaném učiteli se dostaly k Petrovi I. Ruský autokrat potřeboval vzdělané ruské lidi, protože téměř všichni gramotní lidé pocházeli z jiných zemí. Tvůrce zisku Petra I. A.A. Kurbatov představil Teljašina carovi. Císař měl mladého muže velmi rád. Byl ohromen svými znalostmi matematiky. Peter I. dal Leontymu Filippovichovi nové příjmení. Car Petr si vzpomněl na výraz svého duchovního mentora Simeona z Polotsku „Kristus jako magnet přitahuje duše lidí,“ nazval car Petr Teljašina Magnitského – muže, který jako magnet přitahuje poznání. Car Petr jmenoval Leontyho Filippoviče „ruské šlechtické mládeži učitelem matematiky“ na nově otevřené Moskevské plavební škole.

Petr si otevřel matematickou a navigační školu, ale nebyly tam žádné učebnice. Poté car po dobrém uvážení nařídil Leontymu Filippovičovi, aby napsal učebnici aritmetiky.

Magnitskij, opírající se o své nápady pro děti, o příklady a úkoly pro ně vymyšlené, za dva roky vytvořil nejvíce hlavní práce v mém životě - učebnice aritmetiky. Nazval to "Aritmetika - to je číselná věda." Tato kniha vyšla na tehdejší dobu v obrovském nákladu - 2400 výtisků.

Na Navigační škole pracoval Leonty Filippovich jako učitel 38 let - více než polovinu svého života. Byl to skromný člověk, staral se o vědu, staral se o své studenty.

Magnitsky se staral o osud svých studentů, oceňoval jejich talent. V zimě roku 1830 požádal jeden mladý muž Magnitského, aby byl přijat do Navigační školy. Leontyho Filippoviče zarazilo, že se tento mladý muž sám naučil číst z církevních knih a sám překonal matematiku pomocí učebnice „Aritmetika – tedy nauka o číslech“. Magnitského zasáhla skutečnost, že tento mladý muž, stejně jako on, přijel s rybím vlakem do Moskvy. Jméno tohoto mladého muže bylo Michailo Lomonosov. Leonty Filippovich, který před sebou hodnotil talent, neopustil mladého muže v Navigační škole, ale poslal Lomonosova, aby studoval na Slovansko-řecko-latinské akademii.

Magnitsky byl úžasně talentovaný: vynikající matematik, první ruský učitel, teolog, politik, státník, spolupracovník Petrův, básník, autor básně "Poslední soud". Magnitsky zemřel ve věku 70 let. Byl pohřben v kostele Grebněvské ikony Matky Boží u Nikolské brány. Magnitského popel našel klid na téměř dvě století vedle ostatků knížat a hrabat (z rodů Ščerbatova, Urusova, Tolstého, Volyňského).

Magnitského aritmetika

Jeden příběh se často opakuje v příbězích o inženýrech Petrovy éry: poté, co dostali úkol od císaře-císaře Petra Alekseeviče, vzali nejprve „Aritmetiku“ LF Magnitského a poté přistoupili k výpočtům. Abychom zjistili, co vynikající ruští vynálezci našli v Magnitského knize, podívejme se na jeho práci. Toto zásadní dílo L. F. Magnitského nemělo po více než půl století v Rusku obdoby. Studovalo se na školách, oslovovaly ho nejširší kruhy lidí usilujících o vzdělání nebo, jak již bylo řečeno, pracujících na jakémkoli technickém problému. Je známo, že MV Lomonosov nazval Magnitského „Aritmetiku“ spolu se Smotritského „Grammatikou“ „bránami svého učení“.

Hned na začátku v předmluvě Magnitskij vysvětlil význam matematiky pro praktickou činnost. Poukázal na její význam pro plavbu, stavebnictví, vojenské záležitosti, to znamená, že zdůraznil hodnotu této vědy pro stát. Kromě toho si všiml výhod matematiky pro obchodníky, řemeslníky, lidi všech úrovní, tedy obecný občanský význam této vědy. Zvláštností Magnitského „Aritmetiky“ bylo, že autor si byl jistý, že Rusové mají velkou žízeň po vědění, že mnozí z nich studují matematiku sami. Pro ně, kteří se zabývají sebevzděláváním, Magnitsky poskytl každému pravidlu, každému typu problému obrovské množství řešených příkladů. Navíc, vzhledem k důležitosti matematiky pro praktickou činnost, Magnitskij zahrnul do své práce materiál o přírodních vědách a technice. Význam „Aritmetiky“ tak přesáhl hranice samotné matematické literatury a získal obecný kulturní vliv a rozvinul vědecký světonázor širokého okruhu čtenářů.

"Aritmetika" se skládá ze dvou knih. První obsahuje pět částí a je přímo věnována aritmetice. Tato část popisuje pravidla číslování, akce s celými čísly, způsoby ověřování. Dále jsou zde pojmenovaná čísla, kterým předchází rozsáhlá část o starověkých židovských, řeckých, římských penězích, obsahuje informace o mírách a vahách v Holandsku, Prusku, o mírách, vahách a penězích moskevského státu. Jsou uvedeny srovnávací tabulky měr, vah, peněz. Tato sekce se vyznačuje velkou přesností, jasností podání, což svědčí o Magnitského hluboké erudici.

Druhá část je věnována zlomkům, třetí a čtvrtá "pravidlovým problémům", pátá základním pravidlům algebraických akcí, průběhů a kořenů. Existuje mnoho příkladů aplikace algebry na vojenské a námořní záležitosti. Pátá část končí úvahou o akcích s desetinnými zlomky, což byla novinka v tehdejší matematické literatuře.

Je třeba říci, že první kniha „Aritmetiky“ obsahuje mnoho materiálu ze starých ruských ručně psaných knih matematické povahy, což svědčí o kulturní kontinuitě a má vzdělávací hodnotu. Autor hojně využívá i zahraniční matematickou literaturu. Magnitského dílo se přitom vyznačuje velkou originalitou. Za prvé, veškerý materiál je uspořádán systematickým způsobem, který neměl místo v jiných vzdělávacích knihách. Za druhé, problémy byly výrazně aktualizovány, mnohé z nich v jiných učebnicích matematiky nenajdete. V Aritmetice konečně moderní číslování vytlačilo abecední a staré počítání (do tmy, legií atd.) bylo nahrazeno počítáním v milionech, miliardách atd. je v poetické podobě. Obecně platí, že v první části aritmetiky se slabičné verše řídí každým pravidlem. Básně složil sám Magnitsky, což potvrzuje myšlenku, že talentovaný člověk je vždy mnohostranný.

L. Magnitsky nazval druhou knihu "Aritmetika" "Astronomická aritmetika". V předmluvě poukázal na její nezbytnost pro Rusko. Bez ní, tvrdil, je nemožné být dobrým inženýrem, zeměměřičem nebo válečníkem a navigátorem. Tato kniha"Aritmetika" se skládá ze tří částí. V první části je uveden další výklad algebry, včetně řešení kvadratických rovnic. Autor podrobně rozebral několik problémů, ve kterých se setkal s lineárními, kvadratickými a bikvadratickými rovnicemi. V druhé části jsou uvedena řešení geometrických úloh pro měření ploch. Mezi nimi - výpočet plochy rovnoběžníku, pravidelných mnohoúhelníků, segmentu kruhu. Kromě toho je uveden způsob výpočtu objemů kruhových těles. Je zde také uveden průměr, povrch a objem Země. Tato část obsahuje některé geometrické věty. Následují matematické vzorce, které umožňují výpočet goniometrické funkce různé úhly. Třetí část obsahuje informace potřebné pro navigátory: tabulky magnetické deklinace, tabulky zeměpisné šířky bodů východu a západu Slunce a Měsíce, souřadnice nejdůležitějších přístavů, hodiny přílivu a odlivu v nich atd. hodnota až do teď. Je třeba poznamenat, že Magnitskij ve své „Aritmetice“ udělal obrovské množství práce na zdokonalení ruské vědecké terminologie. Právě díky tomuto vynikajícímu vědci se do našeho matematického slovníku dostaly pojmy jako "faktor", "součin", "dividenda a podíl", "čtvercové číslo", "průměrné proporcionální číslo", "proporce", "progrese" atd. ....

Je tedy pochopitelné, proč byla "Aritmetika" L. Magnitského více než půl století hodně a pilně studována, proč se stala základem pro řadu kurzů, které vznikly a vyšly později.Vynikající ruští vynálezci se obrátili na Magnitského dílo nejen jako na encyklopedii, referenční knihu, ale mezi řešeními stovek praktických problémů uvedených v knize našli ta, která by mohla poskytnout analogii, prosadit novou plodnou myšlenku, protože tyto problémy měla praktický význam, prokázala schopnosti matematiky hledající dobré technické řešení.

Řešení problému "Kadi pitya" z Magnitského aritmetiky. Úkoly pro „trojité pravidlo“

"Kad pitya"

Jeden člověk bude pít kadi pití ve 14 dnech a se svou ženou bude pít stejné kadi ve 10 dnech a je moudré jíst, v počtu dní, kdy jeho žena bude pít stejné kadi.

Tento problém jsem našel v elektronické podobě učebnice "Aritmetika" spolu s řešením. L.F. Magnitsky to řeší aritmeticky. Tento problém jsem vyřešil 4 způsoby: dvěma z nich aritmeticky, dvěma algebraicky.

Řešení:

1. způsob.

1) 14 ∙ 5 = 70 (dní) - vyrovnává dobu, po kterou člověk vypije hrnec pitya, s dobou, po kterou člověk a jeho žena vypijí stejnou hrnec pitya

2) 10 ∙ 7 = 70 (dní) - vyrovnává dobu, po kterou muž a jeho žena vypijí hrnec pití, s dobou, po kterou člověk vypije stejný qad

3) 70: 14 = 5 (k.) - člověk vypije za 70 dní

4) 70: 10 = 7 (k.) - člověk s manželkou vypije za 70 dní

5) 7−5 = 2 (k.) - manželka vypije za 70 dní

6) 70: 2 = 35 (dní) - manželka bude pít kadi pitya

2. způsob

Na základě toho, že 1 CAD = 839,71L ≈840L

1) 840: 10 = 84 (l) - osoba a manželka vypijí za 1 den

2) 840: 14 = 60 (l) - člověk vypije za 1 den

3) 84-60 = 24 (l) -manželka vypije za 1 den

4) 840: 24 = 35 (dní) - manželka vypije za 1 den

3. způsob

1) 840: 14 = 60 (l) - člověk vypije za 1 den.

2) Ať manželka vypije xl za 1 den, protože člověk vypije kadi pití za 14 dní a s manželkou vypije stejné kadi za 10 dní, uděláme rovnici:

(60 + X) ∙ 10 = 840

60 + X = 840:10

60 + X = 84

X = 84-60

X = 24 (l) -manželka vypije za 1 den

3) 840: 24 = 35 (dní) - manželka vypije hrnec pitya

4. způsob

Nechte manželku vypít x qadi pitya za 1 den, protože za 1 den člověk vypije 1/14 qadi pitya a s manželkou 1/10 qadi pitya, uděláme rovnici:

1) X + 1/14 = 1/10

X = 1/10 - 1/14

X = (14 - 10) / 140 = 4/140 = 1/35 (qadi pitya) - manželka vypije za 1 den

2) 1/35 ∙ 35 = 35/35 = 1 (kadi pitya) - vypije 1 kadi pitya za 35 dní

Ve 3. čtvrtletí jsme v hodinách matematiky začali studovat téma přímých a nepřímo úměrných vztahů. Tento úkol přímo souvisí s tímto tématem. A když jsem analyzoval řešení tohoto problému a podobných problémů uvedených v Magnitského knize, zjistil jsem, že problémy tohoto typu vyřešil pomocí velmi zajímavého pravidla - "Trojitého pravidla".

Toto pravidlo nazval řetězec, protože data byla zapsána do řetězce za účelem mechanizace výpočtů.

Správnost řešení zcela závisí na správnosti záznamu dat problému.

PRAVIDLO: vynásobte druhé a třetí číslo a vydělte součin prvním.

A v hodinách matematiky jsme se rozhodli ověřit, zda toto pravidlo funguje na moderních problémech prezentovaných v učebnici N.Ya. Vilenkin. Nejprve jsme vyřešili problémy vytvořením proporcí a poté jsme zkontrolovali, zda funguje „trojité pravidlo“. Moje spolužáky toto pravidlo velmi zaujalo, všichni byli překvapeni, jak o více než 300 let později funguje na moderní problémy. Některým klukům se zdálo rozhodování podle trojitého pravidla jednodušší a zajímavější.

Zde jsou příklady těchto úkolů.

č. 783. Ocelová koule o objemu 6 kubických centimetrů má hmotnost 46,8 g. Jakou hmotnost má koule z téže oceli, je-li její objem 2,5 kubických centimetrů? (přímá úměrnost)

Řešení.

Podle Magnitského Nowadays

6 – 46,8 – 2,5 (řetězec)

46,8 x 2,5: 6 = 19,5 (g) x == 19,5 (g)

Odpověď: 19,5 gramů.

č. 784. Z 21 kg bavlníkových semen bylo získáno 5,1 kg oleje. Kolik oleje se vyrobí ze 7 kg bavlníkových semen? (přímá úměrnost)

Řešení.

Podle Magnitského Nowadays

21 – 5,1 – 7 (řetězec)

5,1 x 7: 21 = 1,7 (kg) x == 1,7 (kg)

Odpověď: 1,7 kg.

Za 2 rubly si můžete koupit 6 položek. Kolik si můžete koupit za 4 rubly? (přímá úměrnost)

Řešení.

Podle Magnitského Nowadays

2 - 6 - 4 (řetězec)

6 × 4: 2 = 12 (položky) x = 12 (položky)

Odpověď: 12 položek

č. 785. Pro stavbu stadionu vyklidilo místo 5 buldozerů za 210 minut. Jak dlouho by trvalo 7 buldozerům vyčistit tuto oblast? (inverzní poměr)

Řešení.

Podle Magnitského Nowadays

7 - 5 - 210 (řetězec)

210 × 5: 7 = 150 (min) x == 150 (min)

Odpověď: 150 min.

č. 786. K přepravě nákladu bylo zapotřebí 24 vozidel o nosnosti 7,5 t. Kolik vozidel o nosnosti 4,5 t je potřeba k přepravě stejného nákladu? (inverzní úměra).

Řešení.

Podle Magnitského Nowadays

4,5 – 24 – 7,5 (řetězec)

24 × 7,5: 4,5 = 40 (stroje) x == 40 (stroje)

Odpověď: 40 aut.

V horkém dni vypilo 6 sekaček sud kvasu za 8 hodin. Potřebujete vědět, kolik sekaček vypije stejný soudek kvasu za 3 hodiny? (inverzní úměra).

Řešení.

Podle Magnitského Nowadays

3 - 6 - 8 (řetězec)

6 × 8: 3 = 16 (sekačky) x == 16 (sekačky)

Odpověď: 16 sekaček.

Závěr.

V procesu výzkumu Izjistil, že v učebnici Magnitského byla využita tradice ruských matematických rukopisů, ale systém prezentace látky je v ní výrazně vylepšen: zavádějí se definice, provádí se plynulý přechod na novou, objevují se nové oddíly a úkoly, jsou poskytovány další informace.

Byl jsem přesvědčen, že Magnitského „Aritmetika“ hrála důležitou roli v šíření matematických znalostí v Rusku. Ne nadarmo ji Lomonosov nazval „bránou učení“;

Úlohu z Magnitského "Aritmetiky" jsem vyřešil pomocí aritmetických a algebraických metod. Seznámil jsem se s trojím pravidlem pro řešení problémů v přímé a nepřímé úměrnosti.

O své zkušenosti s řešením problému jsem se podělil se svými spolužáky. Vyprávěl jsem jim o životě a díle L.F. Magnitského. A jeho velkým dílem je učebnice „Aritmetika“. Podařilo se zvýšit zájem o matematiku.

Bibliografie

1. Glazer GI Historie matematiky ve škole. Průvodce pro učitele. - M .: "Vzdělávání", 1981..

2. Gnedenko B.V. a další Encyklopedický slovník mladého matematika.

M.: "Pedagogika", 1985

3. Magnitský L.F. Aritmetika je elektronická verze.

3. Olekhnik SN aj. Antické zábavné úkoly - 3. vyd. - M.: "Drop", 2006.

4.http: //www.etudes.ru/ru/mov/magn/index.php

Školní a pedagogické myšlení v Rusko XVIII proti.
- Osvícenství v Rusku na počátku 18. století.
  - Osvícenství v Rusku na počátku 18. století. - strana 2
  - Osvícenství v Rusku na počátku 18. století. - strana 3
- L.F. Magnitského
  - L.F. Magnitsky - strana 2
  - L.F. Magnitsky - strana 3
- V.N. Tatiščev a začátek odborné vzdělání v Rusku
  - V.N. Tatishchev a začátek odborného vzdělávání v Rusku - strana 2
- Vzdělání a škola po Petru I
- Pedagogická činnost M.V. Lomonosov
  - Pedagogická činnost M.V. Lomonosov - strana 2
  - Pedagogická činnost M.V. Lomonosov - strana 3
- Osvícení v Rusku za éry Kateřiny Veliké
- Pedagogické názory a činnost I.I. Betsky
  - Pedagogické názory a činnost I.I. Betskoy - strana 2
  - Pedagogické názory a činnost I.I. Betskoy - strana 3
  - Pedagogické názory a činnost I.I. Betskoy - strana 4
  - Pedagogické názory a činnost I.I. Betskoy - strana 5
Školské a pedagogické myšlení v západní Evropě a USA v 19. století. (do 90. let)
- Vývoj školy v XIX století. (do 90. let)
  - Vývoj školy v XIX století. (do 90. let) - strana 2
  - Vývoj školy v XIX století. (do 90. let) - strana 3
- Pedagogické myšlení v západní Evropě v 90. letech 19. století.
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 2
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 3
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 4
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 5
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 6
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 7
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 8
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 9
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 10
  - Pedagogické myšlení v západní Evropě v 90. letech 19. století. - strana 11
- Školské a pedagogické myšlení v USA 19. století. (do 90. let)
  - Školské a pedagogické myšlení v USA v 19. století. (do 90. let) - strana 2
  - Školské a pedagogické myšlení v USA v 19. století. (do 90. let) - strana 3
- Problematika vzdělávání v evropských sociálních doktrínách
  - Otázky vzdělávání v evropských sociálních doktrínách - strana 2
  - Otázky vzdělávání v evropských sociálních doktrínách - strana 3
- Myšlenka třídního přístupu k výchově a vzdělávání
  - Myšlenka třídního přístupu k výchově a vzdělávání - strana 2
  - Myšlenka třídního přístupu k výchově a vzdělávání - strana 3
Školské a pedagogické myšlení v Rusku do 90. let 19. století.
- Rozvoj školy a formování školského systému
  - Rozvoj školy a formování školského systému - strana 2
  - Rozvoj školy a formování školského systému - strana 3
  - Rozvoj školy a formování školského systému - strana 4
  - Rozvoj školy a formování školského systému - strana 5
- Pedagogické myšlení v Rusku v 19. století (do 90. let)
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 2
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 3
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 4
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 5
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 6
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 7
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 8
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 9
  - Pedagogické myšlení v Rusku v 19. století (do 90. let) - strana 10
Zahraniční škola a pedagogika koncem XIX - začátkem XX století.
- Školské reformní hnutí na konci 19. století
- Hlavní představitelé reformní pedagogiky
  - Hlavní představitelé reformní pedagogiky - strana 2
  - Hlavní představitelé reformní pedagogiky - strana 3
  - Hlavní představitelé reformní pedagogiky - strana 4
  - Hlavní představitelé reformní pedagogiky - strana 5
- Zkušenosti s organizováním škol podle myšlenek reformní pedagogiky
  - Zkušenosti s organizováním škol na základě myšlenek reformní pedagogiky - strana 2
  - Zkušenosti s organizováním škol na základě myšlenek reformní pedagogiky - strana 3
  - Zkušenosti s organizováním škol na základě myšlenek reformní pedagogiky - strana 4
Škola a pedagogika v Rusku koncem 19. - začátkem 20. století. (do roku 1917)
- Veřejné školství v Rusku koncem 19. - začátkem 20. století.
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 2
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 3
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 4
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 5
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 6
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 7
  - Veřejné školství v Rusku koncem 19. - začátkem 20. století. - strana 8
- Pedagogické myšlení v Rusku na konci XIX - začátku XX století.
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 2
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 3
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 4
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 5
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 6
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 7
  - Pedagogické myšlení v Rusku na konci XIX - začátku XX století. - strana 8
  - Pedagogické myšlení v Rusku na konci XIX - začátku XX století. - strana 9
  - Pedagogické myšlení v Rusku na konci 19. - začátku 20. století. - strana 10
Škola a pedagogika v západní Evropě a USA mezi první a druhou světovou válkou (1918-1939)
- Škola a pedagogika v západní Evropě a USA mezi světovými válkami
  - Škola a pedagogika v západní Evropě a USA mezi světovými válkami - strana 2
  - Škola a pedagogika v západní Evropě a USA mezi světovými válkami - strana 3
  - Škola a pedagogika v západní Evropě a USA mezi světovými válkami - strana 4
  - Škola a pedagogika v západní Evropě a USA mezi světovými válkami - strana 5
  - Škola a pedagogika v západní Evropě a USA mezi světovými válkami - strana 6
Škola v Rusku s únorová revoluce až do konce Velké Vlastenecká válka
- Všeobecné vzdělání po únorové revoluci a říjnové revoluci 1917
  - Všeobecné vzdělání po únorové revoluci a říjnovém převratu 1917 - strana 2
  - Všeobecné vzdělání po únorové revoluci a říjnovém převratu 1917 - strana 3
  - Všeobecné vzdělání po únorové revoluci a říjnovém převratu 1917 - strana 4
  - Všeobecné vzdělání po únorové revoluci a říjnovém převratu 1917 - strana 5
- Problematika obsahu a metod vyučování a výchovné práce ve škole 20. let
  - Problémy obsahu a metod vyučování a výchovné práce ve škole 20. let - strana 2
  - Problémy obsahu a metod vyučování a výchovné práce ve škole 20. let - strana 3
- Pedagogická věda v Rusku po roce 1918
  - Pedagogická věda v Rusku po roce 1918 - strana 2
  - Pedagogická věda v Rusku po roce 1918 - strana 3
  - Pedagogická věda v Rusku po roce 1918 - strana 4
  - Pedagogická věda v Rusku po roce 1918 - strana 5
  - Pedagogická věda v Rusku po roce 1918 - strana 6
  - Pedagogická věda v Rusku po roce 1918 - strana 7
  - Pedagogická věda v Rusku po roce 1918 - strana 8
  - Pedagogická věda v Rusku po roce 1918 - strana 9
- Pedagogická věda za Velké vlastenecké války
  - Pedagogická věda za Velké vlastenecké války - strana 2

L.F. Magnitského

Leonty Filippovich Magnitsky (1669-1739) výrazně přispěl k metodice sekulárního školního vzdělávání éry Petra Velikého a ke školení domácího personálu. Podle tradice, která vzešla od mistrů gramotnosti z moskevské Rusi, vytvořil svou vlastní učebnici - "Aritmetika, to je nauka o číslech," - vydal ji po dvou letech praktického testování v roce 1703. Tato naučná kniha zn. zrod opravdu nové učebnice, která se spojila v sobě národní tradice s výdobytky západoevropských metod výuky exaktních věd. Aritmetický L.F. Magnitsky byl hlavní vzdělávací knihou v matematice až do poloviny 18. století, podle níž M.V. Lomonosov.

Učebnice L.F. Magnitskij měl charakter aplikované, vlastně až utilitární učebnice pro výuku všech základních matematických operací, včetně algebraických, geometrických, trigonometrických a logaritmických. Žáci plavební školy opisovali obsah učebnice, vzorce a kresby na břidlicové tabule, ovládali nikoli teoreticky, ale prakticky vyjmenované obory matematiky.

L.F. Magnitsky různé způsoby vizualizace. Součástí výukového programu byly různé tabulky a rozvržení. Plavební škola používala širokou škálu názorných pomůcek - modely lodí, rytiny, kresby, nástroje, kresby atd.

Již titulní strana „Aritmetiky“ byla jakousi symbolickou názornou pomůckou, která odrážela obsah učebnice, což školákům do jisté míry usnadnilo zvládnutí matematiky, neboť samotný text byl psán jazykem, který děti obtížně ovládaly. rozumět. Samotná aritmetika jako věda byla zobrazena v podobě alegorické ženské postavy s žezlem - klíčem a mocí, sedící na trůnu, k němuž vedou schody se sekvenčním výpisem aritmetických operací: „číslo, sčítání , odčítání, násobení, dělení“. Trůn byl umístěn v „chrámu věd“, jehož klenby nesou dvě skupiny sloupů po čtyřech. První skupina sloupců měla nápisy: "geometrie, stereometrie, astronomie, optika" a spočívala na základu, na kterém byla napsána otázka: "Co dává aritmetika?" Na druhé skupině sloupů byly nápisy: "Mercatorium (jak se tehdy říkalo plavebním vědám), geografie, opevnění, architektura."

„Aritmetika“ LF Magnitského byla v podstatě jakousi matematickou encyklopedií, která měla výrazný aplikovaný charakter. Tato učebnice znamenala začátek zásadně nové generace vzdělávacích knih. Nejenže nebyla horší než západoevropské modely, ale byla také sestavena v hlavním proudu ruské tradice pro ruské studenty.

L.F. Magnitsky dohlížel na celou vzdělávací práci školy, počínaje jejím prvním stupněm. Pro přípravu žáků na výuku v samotné plavební škole byly pod ní zřízeny dvě základní třídy, které se nazývaly „ruská škola“, kde se vyučovalo čtení a psaní v ruštině, a „digitální škola“, kde se děti seznamovaly s tzv. počátky aritmetiky a pro ty, kdo si přejí, aby se učili, ještě šerm.

Všechny akademické předměty se v navigační škole studovaly postupně, neprobíhaly žádné přestupy a závěrečné zkoušky, studenti byli převáděni z třídy do třídy tak, jak se učili, a samotný pojem „třída“ neznamenal prvek systému třída-lekce, který ještě nebyl v Rusku, ale obsah vzdělávání : hodina navigace, hodina geometrie atd. Ze školy byli propuštěni, jakmile byl žák připraven na konkrétní státní činnost nebo na žádost různých kateder, které nutně potřebovaly vzdělané odborníky. Na uvolněné místo byli okamžitě přijati noví studenti.

Stránky: 1 2 3