વેક્ટર્સ: વ્યાખ્યા અને મૂળભૂત ખ્યાલો. કમ્પ્યુટર રમતોમાં વેક્ટર પડેલા વેક્ટર

અમે હજી આ સૂત્રની વિગતવાર ચર્ચા કરીશું નહીં. ઉપરાંત, તે યાદ રાખવું ખૂબ મુશ્કેલ છે. નિર્ધારકો સાથે પરિચિત થયા પછી અમે આ મુદ્દા પર પાછા આવીશું.

ઠીક છે, સામાન્ય વિકાસ માટે, તે જાણવું ઉપયોગી છે કે પરિણામી વેક્ટરની લંબાઈ વેક્ટર પર બનેલા સમાંતરગ્રામના ક્ષેત્રફળ જેટલી છે. aઅને b.

વેક્ટર નોર્મલાઇઝેશન

સામાન્યકૃત વેક્ટર એ વેક્ટર છે જેની લંબાઈ એક છે.

સામાન્યકૃત વેક્ટર શોધવા માટેનું સૂત્ર નીચે મુજબ છે - વેક્ટરના તમામ ઘટકો તેની લંબાઈથી વિભાજિત હોવા જોઈએ:

વિ n = વિ/|વ| =

આફ્ટરવર્ડ

જેમ તમે કદાચ જોયું હશે, વેક્ટરને સમજવું મુશ્કેલ નથી. અમે સંખ્યાબંધ વેક્ટર કામગીરીને આવરી લીધી છે.

"ગણિત" વિભાગના આગામી લેખોમાં, આપણે મેટ્રિસીસ, નિર્ધારકો, રેખીય સમીકરણોની પ્રણાલીઓની ચર્ચા કરીશું. આ બધો સિદ્ધાંત છે.

તે પછી, આપણે મેટ્રિક્સ ટ્રાન્સફોર્મેશન્સ જોઈશું. તે પછી જ તમે સમજી શકશો કે કમ્પ્યુટર રમતો બનાવવા માટે ગણિત કેટલું મહત્વપૂર્ણ છે. આ વિષય ફક્ત અગાઉના તમામ વિષયો માટે પ્રેક્ટિસ બની જશે.

વ્યાખ્યા ઓર્ડર કરેલ સંગ્રહ (x 1, x 2, ..., x n) n વાસ્તવિક સંખ્યાઓ કહેવાય છે n-પરિમાણીય વેક્ટર, અને સંખ્યાઓ x i (i = 1, ..., n) છે ઘટકોઅથવા સંકલન,

ઉદાહરણ. જો, ઉદાહરણ તરીકે, કોઈ ચોક્કસ ઓટોમોબાઈલ પ્લાન્ટમાં 50 કાર, 100 ટ્રક, 10 બસ, કારના સ્પેરપાર્ટ્સના 50 સેટ અને ટ્રક અને બસો માટે 150 સેટ પ્રતિ શિફ્ટ બનાવવાના હોય, તો આ પ્લાન્ટનો પ્રોડક્શન પ્રોગ્રામ આમાં લખી શકાય. વેક્ટરનું સ્વરૂપ (50, 100, 10, 50, 150) જેમાં પાંચ ઘટકો છે.

નોટેશન. વેક્ટર્સને બોલ્ડ લોઅરકેસ અક્ષરોમાં અથવા ટોચ પર બાર અથવા તીરવાળા અક્ષરોમાં સૂચવવામાં આવે છે, ઉદાહરણ તરીકે, aઅથવા બે વેક્ટર કહેવાય છે સમાનજો તેમની પાસે ઘટકોની સમાન સંખ્યા હોય અને તેમના અનુરૂપ ઘટકો સમાન હોય.

વેક્ટર ઘટકોને સ્વેપ કરી શકાતા નથી, ઉદાહરણ તરીકે, (3, 2, 5, 0, 1) અને (2, 3, 5, 0, 1) અલગ-અલગ વેક્ટર છે.
વેક્ટર પર કામગીરી.ઉત્પાદન દ્વારાx= (x 1, x 2, ..., x n) વાસ્તવિક સંખ્યા λ દ્વારા વેક્ટર કહેવાય છે λ x= (λ x 1, λ x 2, ..., λ x n).

રકમx= (x 1, x 2, ..., x n) અને y= (y 1, y 2, ..., y n) વેક્ટર કહેવાય છે x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

વેક્ટરની જગ્યા.એન-પરિમાણીય વેક્ટર જગ્યા આર n એ તમામ n-પરિમાણીય વેક્ટર્સના સમૂહ તરીકે વ્યાખ્યાયિત કરવામાં આવે છે જેના માટે વાસ્તવિક સંખ્યાઓ અને ઉમેરા દ્વારા ગુણાકારની ક્રિયાઓ વ્યાખ્યાયિત કરવામાં આવે છે.

આર્થિક ચિત્ર. એન-ડાયમેન્શનલ વેક્ટર સ્પેસનું આર્થિક ચિત્ર: માલની જગ્યા (માલ). હેઠળ કોમોડિટીઅમે કેટલીક સારી અથવા સેવા સમજીશું જે ચોક્કસ સમયે ચોક્કસ જગ્યાએ વેચાણ પર હતી. ધારો કે હાથ પર વસ્તુઓની મર્યાદિત સંખ્યા છે, n; ઉપભોક્તા દ્વારા ખરીદેલ તેમાંથી દરેકની માત્રા માલના સમૂહ દ્વારા વર્ગીકૃત થયેલ છે

x= (x 1, x 2, ..., x n),

જ્યાં x i ઉપભોક્તા દ્વારા ખરીદેલ i-th ગુડની રકમ દર્શાવે છે. અમે ધારીશું કે તમામ માલસામાનમાં મનસ્વી વિભાજનની મિલકત છે, જેથી તેમાંથી દરેકની કોઈપણ બિન-નકારાત્મક રકમ ખરીદી શકાય. પછી માલના તમામ સંભવિત સમૂહો માલની જગ્યાના વેક્ટર છે C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

રેખીય સ્વતંત્રતા. સિસ્ટમ ઇ 1 , ઇ 2 , ... , ઇ m n-પરિમાણીય વેક્ટર કહેવાય છે રેખીય રીતે નિર્ભરજો ત્યાં સંખ્યાઓ λ 1, λ 2, ..., λ m એવી હોય કે તેમાંથી ઓછામાં ઓછી એક શૂન્ય ન હોય જેમ કે λ 1 ઇ 1 + λ મી ઇ m = 0; અન્યથા, આ વેક્ટર સિસ્ટમ કહેવાય છે રેખીય રીતે સ્વતંત્ર, એટલે કે, દર્શાવેલ સમાનતા ફક્ત ત્યારે જ શક્ય છે જ્યારે બધા λ 1 = λ 2 = ... = λ m = 0 હોય. માં વેક્ટર્સની રેખીય અવલંબનનો ભૌમિતિક અર્થ આર 3, નિર્દેશિત વિભાગો તરીકે અર્થઘટન, નીચેના પ્રમેય સમજાવો.

પ્રમેય 1. એક વેક્ટર ધરાવતી સિસ્ટમ રેખીય રીતે નિર્ભર છે જો અને માત્ર જો આ વેક્ટર શૂન્ય હોય.

પ્રમેય 2. બે વેક્ટર્સ રેખીય રીતે નિર્ભર રહેવા માટે, તે જરૂરી અને પૂરતું છે કે તેઓ સમરેખીય (સમાંતર) હોય.

પ્રમેય 3 ... ત્રણ વેક્ટર રેખીય રીતે આશ્રિત રહેવા માટે, તે જરૂરી અને પર્યાપ્ત છે કે તેઓ કોપ્લાનર (એક જ સમતલમાં આવેલા) હોય.

વેક્ટરની ડાબી અને જમણી ત્રિપુટી. ત્રણ નોન-કોપ્લાનર વેક્ટર a, b, cકહેવાય છે અધિકારજો તેમના સામાન્ય મૂળમાંથી નિરીક્ષક વેક્ટરના છેડાને પસાર કરે છે a, b, cબતાવેલ ક્રમમાં, તે ઘડિયાળની દિશામાં હોય તેવું લાગે છે. અન્યથા a, b, c -ડાબી ત્રણ... વેક્ટરના બધા જમણા (અથવા ડાબે) ત્રિપુટી કહેવામાં આવે છે સમાન રીતે લક્ષી.

આધાર અને સંકલન. ટ્રોઇકા ઇ 1, ઇ 2 , ઇમાં 3 નોન-કોપ્લાનર વેક્ટર આર 3 કહેવાય છે આધાર, અને વેક્ટર પોતે ઇ 1, ઇ 2 , ઇ 3 - પાયાની... કોઈપણ વેક્ટર aઆધાર વેક્ટરની દ્રષ્ટિએ વિશિષ્ટ રીતે વિસ્તૃત કરી શકાય છે, એટલે કે, ફોર્મમાં રજૂ થાય છે

a= x 1 ઇ 1 + x 2 ઇ 2 + x 3 ઇ 3, (1.1)

વિસ્તરણ (1.1) માં x 1, x 2, x 3 નંબરો કહેવામાં આવે છે સંકલનaઆધાર માં ઇ 1, ઇ 2 , ઇ 3 અને સૂચવવામાં આવે છે a(x 1, x 2, x 3).

ઓર્થોનોર્મલ આધાર. જો વેક્ટર્સ ઇ 1, ઇ 2 , ઇ 3 જોડી પ્રમાણે લંબ છે અને તે દરેકની લંબાઈ એક સમાન છે, તો આધાર કહેવાય છે ઓર્થોનોર્મલ, અને સંકલન x 1, x 2, x 3 - લંબચોરસઓર્થોનોર્મલ આધારના આધાર વેક્ટર દ્વારા સૂચિત કરવામાં આવશે i, j, k.

અમે તેને અવકાશમાં ધારીશું આર 3 કાર્ટેશિયન લંબચોરસ કોઓર્ડિનેટ્સની યોગ્ય સિસ્ટમ પસંદ કરવામાં આવી છે (0, i, j, k}.

વેક્ટર ઉત્પાદન.વેક્ટર ઉત્પાદનaવેક્ટર દીઠ bવેક્ટર કહેવાય છે c, જે નીચેની ત્રણ શરતો દ્વારા નક્કી કરવામાં આવે છે:

1. વેક્ટર લંબાઈ cસંખ્યાત્મક રીતે વેક્ટર પર બનેલ સમાંતરગ્રામના ક્ષેત્રફળની બરાબર છે aઅને bએટલે કે
c= | એ || બી |પાપ ( a^b).

2. વેક્ટર cદરેક વેક્ટરને લંબરૂપ aઅને b

3. વેક્ટર a bઅને cસૂચવેલ ક્રમમાં જમણા હાથની ત્રિપુટી બનાવે છે.

વેક્ટર ઉત્પાદન માટે cનોટેશન રજૂ કરવામાં આવે છે c =[ab] અથવા
c = a × b

જો વેક્ટર્સ aઅને bસમરેખા, પછી પાપ ( a ^ b) = 0 અને [ ab] = 0, ખાસ કરીને, [ aa] = 0. એકમ વેક્ટરના વેક્ટર ઉત્પાદનો: [ ij]=k, [જેકે] = i, [કી]=j.

જો વેક્ટર્સ aઅને bઆધારે આપવામાં આવે છે i, j, kસંકલન a(a 1, a 2, a 3) b(b 1, b 2, b 3), પછી

મિશ્ર કાર્ય. જો બે વેક્ટરનું ક્રોસ ઉત્પાદન aઅને bસ્કેલર ત્રીજા વેક્ટર દ્વારા ગુણાકાર c,પછી ત્રણ વેક્ટરના આવા ઉત્પાદનને કહેવામાં આવે છે મિશ્ર કાર્યઅને પ્રતીક દ્વારા સૂચવવામાં આવે છે a b c.

જો વેક્ટર્સ a, bઅને cઆધાર માં i, j, kતેમના કોઓર્ડિનેટ્સ દ્વારા આપવામાં આવે છે
a(a 1, a 2, a 3) b(b 1, b 2, b 3), c(c 1, c 2, c 3), પછી

.

મિશ્ર ઉત્પાદનમાં એક સરળ ભૌમિતિક અર્થઘટન છે - તે આ ત્રણ વેક્ટર પર બનેલ સમાંતર પાઇપના જથ્થાના ચોક્કસ મૂલ્યમાં સમાન સ્કેલર છે.

જો વેક્ટર્સ જમણા હાથની ત્રિપુટી બનાવે છે, તો તેમનું મિશ્રિત ઉત્પાદન સૂચવેલ વોલ્યુમની બરાબર હકારાત્મક સંખ્યા છે; જો ત્રણ a, b, c -બાકી, પછી a b c<0 и V = - a b c, તેથી V = |અ બી સી |.

પ્રથમ પ્રકરણની સમસ્યાઓમાં વેક્ટરના કોઓર્ડિનેટ્સ યોગ્ય ઓર્થોનોર્મલ આધારના સંદર્ભમાં આપવામાં આવ્યા હોવાનું માનવામાં આવે છે. વેક્ટર માટે એકમ વેક્ટર કોડાયરેક્શનલ aપ્રતીક દ્વારા સૂચવવામાં આવે છે aઓ. પ્રતીક આર=ઓમબિંદુ M ના ત્રિજ્યા વેક્ટર દ્વારા સૂચિત, પ્રતીકો a, AB અથવા |અ |, |એબી |વેક્ટરના મોડ્યુલો aઅને એબી.

ઉદાહરણ 1.2. વેક્ટર વચ્ચેનો ખૂણો શોધો a= 2m+4nઅને b= m-n, ક્યાં mઅને n -એકમ વેક્ટર અને વચ્ચેનો કોણ mઅને n 120 p ની બરાબર છે.

ઉકેલ... અમારી પાસે છે: cos φ = ab/ ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0.5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0.5) + 16 = 12, તેથી a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0.5) +1 = 3, તેથી b =. છેલ્લે, આપણી પાસે છે: cos φ == -1/2, φ = 120 o.

ઉદાહરણ 1.3.વેક્ટર્સ જાણતા એબી(-3, -2.6) અને પૂર્વે(-2,4,4), ત્રિકોણ ABC ની ઊંચાઈ AD ની લંબાઈની ગણતરી કરો.

ઉકેલ... S દ્વારા ત્રિકોણ ABC ના ક્ષેત્રફળ દર્શાવતા, આપણને મળે છે:
S = 1/2 BC AD. પછી AD = 2S/BC, BC = = = 6,
S = 1/2 | એબી ×એસી |. AC = AB + BC, તેથી વેક્ટર એસીકોઓર્ડિનેટ્સ ધરાવે છે
.

વેક્ટર
ભૌતિકશાસ્ત્ર અને ગણિતમાં, વેક્ટર એ એક જથ્થો છે જે તેના સંખ્યાત્મક મૂલ્ય અને દિશા દ્વારા વર્ગીકૃત થયેલ છે. ભૌતિકશાસ્ત્રમાં, ઘણા મહત્વપૂર્ણ જથ્થાઓ છે જે વેક્ટર્સ છે, ઉદાહરણ તરીકે, બળ, સ્થિતિ, ગતિ, પ્રવેગક, ટોર્ક, વેગ, ઇલેક્ટ્રિક અને ચુંબકીય ક્ષેત્રોની તાકાત. તેઓ અન્ય જથ્થાઓ જેમ કે સમૂહ, વોલ્યુમ, દબાણ, તાપમાન અને ઘનતા સાથે વિરોધાભાસી હોઈ શકે છે, જે સામાન્ય સંખ્યા દ્વારા વર્ણવી શકાય છે, અને તેમને "સ્કેલર્સ" કહેવામાં આવે છે. વેક્ટર નોટેશનનો ઉપયોગ મૂલ્યો સાથે કામ કરતી વખતે થાય છે જે સામાન્ય સંખ્યાઓનો ઉપયોગ કરીને સંપૂર્ણ રીતે સ્પષ્ટ કરી શકાતા નથી. ઉદાહરણ તરીકે, આપણે અમુક બિંદુને લગતી વસ્તુની સ્થિતિનું વર્ણન કરવા માંગીએ છીએ. આપણે કહી શકીએ છીએ કે કોઈ બિંદુથી કોઈ વસ્તુ સુધી કેટલા કિલોમીટર છે, પરંતુ જ્યાં સુધી તે સ્થિત છે તે દિશામાં આપણે જાણીએ નહીં ત્યાં સુધી અમે તેનું સ્થાન સંપૂર્ણપણે નિર્ધારિત કરી શકતા નથી. આમ, ઑબ્જેક્ટનું સ્થાન સંખ્યાત્મક મૂલ્ય (કિલોમીટરમાં અંતર) અને દિશા દ્વારા વર્ગીકૃત થયેલ છે. ગ્રાફિકલી રીતે, વેક્ટર્સને ફિગની જેમ ચોક્કસ લંબાઈના નિર્દેશિત સીધા રેખા સેગમેન્ટ્સ તરીકે દર્શાવવામાં આવ્યા છે. 1. ઉદાહરણ તરીકે, પાંચ કિલોગ્રામના બળને ગ્રાફિકલી રીતે દર્શાવવા માટે, તમારે બળની દિશામાં પાંચ એકમો લાંબો એક સીધી રેખા સેગમેન્ટ દોરવાની જરૂર છે. તીર સૂચવે છે કે બળ A થી B સુધી કાર્ય કરી રહ્યું છે; જો બળ B થી A સુધી કાર્ય કરે છે, તો પછી આપણે લખીશું અથવા સગવડ માટે, વેક્ટર સામાન્ય રીતે બોલ્ડ કેપિટલ અક્ષરોમાં સૂચવવામાં આવે છે (A, B, C, અને તેથી વધુ); વેક્ટર A અને -A સમાન સંખ્યાત્મક મૂલ્યો ધરાવે છે, પરંતુ દિશામાં વિરુદ્ધ છે. વેક્ટર A ના સંખ્યાત્મક મૂલ્યને મોડ્યુલસ અથવા લંબાઈ કહેવામાં આવે છે અને તેને A અથવા | A | દ્વારા સૂચિત કરવામાં આવે છે. આ જથ્થો, અલબત્ત, એક સ્કેલર છે. એક વેક્ટર જેની શરૂઆત અને અંત એકરૂપ થાય છે તેને શૂન્ય કહેવામાં આવે છે અને તેને O દ્વારા સૂચિત કરવામાં આવે છે.

બે વેક્ટરને સમાન (અથવા મુક્ત) કહેવામાં આવે છે જો તેમના મોડ્યુલો અને દિશાઓ એકરૂપ થાય. મિકેનિક્સ અને ભૌતિકશાસ્ત્રમાં, આ વ્યાખ્યાનો ઉપયોગ સાવધાની સાથે થવો જોઈએ, કારણ કે સામાન્ય કિસ્સામાં શરીરના જુદા જુદા બિંદુઓ પર બે સમાન દળો લાગુ થવાથી વિવિધ પરિણામો આવશે. આ સંદર્ભમાં, વેક્ટર્સને "લિંક્ડ" અથવા "સ્લાઇડિંગ" માં વર્ગીકૃત કરવામાં આવે છે, જે નીચે મુજબ છે: લિંક્ડ વેક્ટર્સમાં એપ્લિકેશનના નિશ્ચિત બિંદુઓ હોય છે. ઉદાહરણ તરીકે, ત્રિજ્યા વેક્ટર અમુક નિશ્ચિત મૂળની તુલનામાં બિંદુની સ્થિતિ સૂચવે છે. સંબંધિત વેક્ટર્સને સમાન ગણવામાં આવે છે જો તેમની પાસે માત્ર સમાન મોડ્યુલો અને દિશાઓ જ ન હોય, પરંતુ તેમની પાસે એક સામાન્ય બિંદુ પણ હોય. સ્લાઇડિંગ વેક્ટર એ એક સીધી રેખા પર સ્થિત સમાન વેક્ટર છે.
વેક્ટર્સનો ઉમેરો.વેક્ટર્સ ઉમેરવાનો વિચાર એ હકીકત પરથી ઉદ્ભવ્યો છે કે આપણે એક વેક્ટર શોધી શકીએ છીએ જે અન્ય બે વેક્ટરની સમાન અસર ધરાવે છે. જો, ચોક્કસ બિંદુ સુધી પહોંચવા માટે, આપણે એક દિશામાં પહેલા A કિલોમીટર અને પછી બીજી દિશામાં B કિલોમીટર ચાલવાની જરૂર હોય, તો પછી આપણે ત્રીજી દિશામાં C કિલોમીટર પસાર કર્યા પછી અમારા અંતિમ બિંદુ સુધી પહોંચી શકીએ (ફિગ. 2) . આ અર્થમાં આપણે એમ કહી શકીએ

અમે કોઈપણ સંખ્યાના વેક્ટર ઉમેરી શકીએ છીએ, અને શરતોનો ક્રમ પરિણામને અસર કરતું નથી. વાતચીત પણ સાચી છે: કોઈપણ વેક્ટર બે અથવા વધુ "ઘટકો" માં વિઘટિત થાય છે, એટલે કે. બે અથવા વધુ વેક્ટરમાં, જે ઉમેરવામાં આવે ત્યારે, પરિણામ તરીકે મૂળ વેક્ટર આપશે. ઉદાહરણ તરીકે, ફિગમાં. 2, A અને B એ C ઘટકો છે. જો વેક્ટરને ત્રણ પરસ્પર લંબ દિશામાં ત્રણ ઘટકોમાં વિઘટિત કરવામાં આવે તો વેક્ટર સાથેની ઘણી ગાણિતિક ક્રિયાઓ સરળ બને છે. ચાલો ફિગમાં બતાવ્યા પ્રમાણે Ox, Oy અને Oz અક્ષો સાથે જમણા હાથની કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ પસંદ કરીએ. 5. જમણી સંકલન પ્રણાલી દ્વારા, અમારો અર્થ એ છે કે x, y અને z અક્ષો અનુક્રમે જમણા હાથના અંગૂઠા, તર્જની અને મધ્ય આંગળીઓ સ્થિત થઈ શકે તે જ રીતે સ્થિત છે. એક જમણા હાથની કોઓર્ડિનેટ સિસ્ટમમાંથી, તમે હંમેશા અન્ય જમણા હાથની સંકલન સિસ્ટમને તે મુજબ ફેરવીને મેળવી શકો છો. અંજીરમાં. 5, વેક્ટર A નું ત્રણ ઘટકોમાં વિઘટન દર્શાવવામાં આવ્યું છે, અને તેઓ વેક્ટર A સાથે ઉમેરે છે, કારણ કે

આથી,

તમે ત્રણ સંકલન અક્ષો પર વેક્ટર A ના અનુમાનોમાં પહેલા ઉમેરી અને મેળવી શકો છો અને પછી ઉમેરી શકો છો, Ax, Ay અને Az ને વેક્ટર A ના "સ્કેલર ઘટકો" કહેવામાં આવે છે:

જ્યાં a, b અને g એ A અને ત્રણ સંકલન અક્ષો વચ્ચેના ખૂણા છે. હવે આપણે એકમ લંબાઈ i, j અને k (એકમ વેક્ટર) ના ત્રણ વેક્ટર રજૂ કરીએ છીએ, જે અનુરૂપ અક્ષો x, y અને z જેવી જ દિશા ધરાવે છે. પછી, જો Ax ને i વડે ગુણાકાર કરવામાં આવે, તો પરિણામી ઉત્પાદન એ અને ની સમાન વેક્ટર છે

બે વેક્ટર સમાન હોય છે જો અને માત્ર જો તેમના અનુરૂપ સ્કેલર ઘટકો સમાન હોય. આમ, A = B જો અને માત્ર જો Ax = Bx, Ay = By, Az = Bz. બે વેક્ટર તેમના ઘટકો ઉમેરીને ઉમેરી શકાય છે:

વધુમાં, પાયથાગોરિયન પ્રમેય દ્વારા:

રેખીય કાર્યો. aA + bB અભિવ્યક્તિ, જ્યાં a અને b સ્કેલર છે, તેને A અને B વેક્ટરનું રેખીય કાર્ય કહેવામાં આવે છે. તે A અને B સમાન સમતલમાં વેક્ટર છે; જો A અને B સમાંતર ન હોય, તો જ્યારે a અને b બદલાય છે, ત્યારે વેક્ટર aA + bB સમગ્ર પ્લેન પર જશે (ફિગ. 6). જો A, B અને C બધા એક જ પ્લેનમાં ન હોય, તો વેક્ટર aA + bB + cC (a, b અને c ફેરફાર) સમગ્ર અવકાશમાં ફરે છે. ધારો કે A, B અને C એકમ વેક્ટર i, j અને k છે. વેક્ટર ai x-અક્ષ પર આવેલું છે; વેક્ટર ai + bj સમગ્ર xy પ્લેન સાથે આગળ વધી શકે છે; વેક્ટર ai + bj + ck સમગ્ર જગ્યામાં ખસેડી શકે છે.

અને કોઈ પાંચ, છ અથવા કોઈપણ સંખ્યાના પરિમાણો સુધી ચાલુ રાખી શકે છે. જો કે આવા વેક્ટરની કલ્પના કરવી અશક્ય છે, અહીં કોઈ ગાણિતિક મુશ્કેલીઓ ઊભી થતી નથી. આવા રેકોર્ડ ઘણીવાર ઉપયોગી છે; ઉદાહરણ તરીકે, ફરતા કણની સ્થિતિનું વર્ણન છ-પરિમાણીય વેક્ટર P (x, y, z, px, py, pz) દ્વારા કરવામાં આવે છે, જેના ઘટકો અવકાશમાં તેની સ્થિતિ (x, y, z) અને વેગ છે. (px, py, pz). આ જગ્યાને "ફેઝ સ્પેસ" કહેવામાં આવે છે; જો આપણે બે કણોને ધ્યાનમાં લઈએ, તો તબક્કા અવકાશ 12-પરિમાણીય છે, જો ત્રણ, તો 18, અને તેથી વધુ. પરિમાણોની સંખ્યા અનિશ્ચિત રૂપે વધારી શકાય છે; જો કે, આપણે જે જથ્થાઓ સાથે વ્યવહાર કરીશું તે તે જ રીતે વર્તે છે જે આપણે આ લેખના બાકીના ભાગમાં ધ્યાનમાં લઈશું, એટલે કે, ત્રિ-પરિમાણીય વેક્ટર.
બે વેક્ટરનો ગુણાકાર.વેક્ટર ઉમેરાનો નિયમ વેક્ટર દ્વારા રજૂ કરાયેલા જથ્થાના વર્તનનો અભ્યાસ કરીને મેળવવામાં આવ્યો હતો. બે વેક્ટરનો કોઈપણ રીતે ગુણાકાર કેમ ન થઈ શકે તેનું કોઈ દેખીતું કારણ નથી, પરંતુ આ ગુણાકાર માત્ર ત્યારે જ અર્થપૂર્ણ બનશે જો તમે તેની ગાણિતિક સુસંગતતા બતાવી શકો; વધુમાં, તે ઇચ્છનીય છે કે કાર્યનો ચોક્કસ ભૌતિક અર્થ હોય. આ શરતોને પૂર્ણ કરતા વેક્ટર્સને ગુણાકાર કરવાની બે રીતો છે. તેમાંથી એકનું પરિણામ સ્કેલર છે, આવા ઉત્પાદનને "ડોટ પ્રોડક્ટ" અથવા બે વેક્ટરનું "આંતરિક ઉત્પાદન" કહેવામાં આવે છે અને ABB અથવા (A, B) લખવામાં આવે છે. અન્ય ગુણાકાર વેક્ટરમાં પરિણમે છે જેને "વેક્ટર ઉત્પાદન" અથવા "બાહ્ય ઉત્પાદન" કહેવામાં આવે છે અને તેને A * B અથવા [] લખવામાં આવે છે. ડોટ પ્રોડક્ટ્સ એક, બે અથવા ત્રણ પરિમાણો માટે ભૌતિક અર્થ ધરાવે છે, જ્યારે વેક્ટર ઉત્પાદનો માત્ર ત્રણ પરિમાણો માટે વ્યાખ્યાયિત કરવામાં આવે છે.
સ્કેલર ઉત્પાદનો.જો, અમુક બળ F ની ક્રિયા હેઠળ, તે જે બિંદુ પર લાગુ થાય છે તે r અંતરે ખસે છે, તો કરવામાં આવેલ કાર્ય r ના ગુણાંક અને r દિશામાં ઘટક F સમાન છે. આ ઘટક F cos bF, rc ની બરાબર છે, જ્યાં bF, rc એ F અને r વચ્ચેનો કોણ છે, એટલે કે. કાર્ય કર્યું = Fr cos bF, rc. આ સૂત્ર દ્વારા કોઈપણ બે વેક્ટર A, B માટે વ્યાખ્યાયિત ડોટ પ્રોડક્ટના ભૌતિક ન્યાયીકરણનું ઉદાહરણ છે.
A * B = AB cos bA, Bc.
સમીકરણની જમણી બાજુના તમામ જથ્થાઓ સ્કેલર હોવાથી, પછી A * B = B * A; તેથી સ્કેલર ગુણાકાર વિનિમયાત્મક છે. સ્કેલર ગુણાકારમાં વિતરણ ગુણધર્મ પણ છે: A * (B + C) = A * B + A * C. જો વેક્ટર A અને B કાટખૂણે હોય, તો cos bA, Bc શૂન્યની બરાબર છે, અને તેથી, A * B = 0, ભલે A કે B બેમાંથી કોઈ શૂન્ય ન હોય. તેથી જ આપણે વેક્ટર દ્વારા ભાગાકાર કરી શકતા નથી. ચાલો કહીએ કે આપણે સમીકરણ A * B = A * C ને A વડે વિભાજિત કર્યા છે. તે B = C આપશે, અને જો ભાગાકાર થઈ શકે, તો આ સમાનતા એકમાત્ર સંભવિત પરિણામ હશે. જો કે, જો આપણે સમીકરણ A * B = A * C ને A * (B - C) = 0 તરીકે ફરીથી લખીએ અને યાદ રાખીએ કે (B - C) એ વેક્ટર છે, તો તે સ્પષ્ટ છે કે (B - C) શૂન્ય નથી. અને, તેથી, B એ C ની બરાબર હોવું જરૂરી નથી. આ વિરોધાભાસી પરિણામો દર્શાવે છે કે વેક્ટર વિભાજન અશક્ય છે. ડોટ પ્રોડક્ટ વેક્ટરનું સંખ્યાત્મક મૂલ્ય (મોડ્યુલસ) લખવાની બીજી રીત આપે છે: A * A = AA * cos 0 ° = A2;
એ કારણે

ડોટ પ્રોડક્ટ બીજી રીતે લખી શકાય. આ કરવા માટે, યાદ રાખો કે: A = Ax i + Ayj + Azk. આ ધ્યાન માં રાખો

પછી,

છેલ્લા સમીકરણમાં સબસ્ક્રીપ્ટ તરીકે x, y અને z શામેલ હોવાથી, સમીકરણ મોટે ભાગે પસંદ કરેલ ચોક્કસ સંકલન પ્રણાલી પર આધાર રાખે છે. જો કે, આ એવું નથી, જેમ કે વ્યાખ્યા પરથી જોઈ શકાય છે, જે પસંદ કરેલ સંકલન અક્ષોથી સ્વતંત્ર છે.
વેક્ટર આર્ટવર્ક.વેક્ટર અથવા વેક્ટરનું બાહ્ય ઉત્પાદન એ એક વેક્ટર છે જેનું મોડ્યુલસ મૂળ વેક્ટરને લંબરૂપ કોણની સાઈન દ્વારા તેમના મોડ્યુલીના ગુણાંક જેટલું હોય છે અને તેમની સાથે જમણી ત્રિપુટી બનાવે છે. વેગ અને કોણીય વેગ વચ્ચેના સંબંધને ધ્યાનમાં લઈને આ ઉત્પાદન રજૂ કરવું સૌથી સરળ છે. પ્રથમ વેક્ટર છે; હવે આપણે બતાવીશું કે બાદમાં વેક્ટર તરીકે પણ અર્થઘટન કરી શકાય છે. ફરતા શરીરનો કોણીય વેગ નીચે પ્રમાણે નક્કી કરવામાં આવે છે: શરીર પર કોઈપણ બિંદુ પસંદ કરો અને આ બિંદુથી પરિભ્રમણની ધરી સુધી લંબ દોરો. પછી શરીરનો કોણીય વેગ એ રેડિયનની સંખ્યા છે જેના દ્વારા આ રેખા સમયના એકમ દીઠ ફેરવાઈ છે. જો કોણીય વેગ એ વેક્ટર છે, તો તેનું સંખ્યાત્મક મૂલ્ય અને દિશા હોવી આવશ્યક છે. સંખ્યાત્મક મૂલ્ય રેડિયન પ્રતિ સેકન્ડમાં દર્શાવવામાં આવે છે, પરિભ્રમણની અક્ષ સાથે દિશા પસંદ કરી શકાય છે, તમે વેક્ટરને તે દિશામાં દિશામાન કરીને નિર્ધારિત કરી શકો છો કે જેમાં શરીર સાથે ફરતી વખતે જમણા હાથનો સ્ક્રૂ ખસેડશે. નિશ્ચિત ધરીની આસપાસ શરીરના પરિભ્રમણને ધ્યાનમાં લો. જો આપણે આ અક્ષને રીંગની અંદર સ્થાપિત કરીએ, જે બદલામાં બીજી રીંગની અંદર દાખલ કરેલ ધરી પર સ્થિર થાય છે, તો આપણે પ્રથમ રીંગની અંદરના શરીરને કોણીય વેગ w1 પર ફેરવી શકીએ છીએ અને પછી આંતરિક રીંગ (અને શરીરને) એક પર ફેરવી શકીએ છીએ. કોણીય વેગ w2. આકૃતિ 7 બિંદુ સમજાવે છે; ગોળાકાર તીરો પરિભ્રમણની દિશાઓ દર્શાવે છે. આ શરીર કેન્દ્ર O અને ત્રિજ્યા r સાથેનો ઘન ગોળો છે.

ચોખા. 7. કેન્દ્ર O સાથેનો ગોળો, રિંગ BC ની અંદર કોણીય વેગ w1 સાથે ફરે છે, જે બદલામાં, કોણીય વેગ w2 સાથે રિંગ DE ની અંદર ફરે છે. ગોળા કોણીય વેગના સરવાળા સમાન કોણીય વેગ સાથે ફરે છે, અને સીધી રેખા POP" પરના તમામ બિંદુઓ તાત્કાલિક આરામની સ્થિતિમાં છે.

આ અંતર શૂન્ય છે જો

આ કિસ્સામાં, બિંદુ P ત્વરિત આરામની સ્થિતિમાં હોય છે, અને તે જ રીતે POP રેખા પરના તમામ બિંદુઓ. "બાકીનો ગોળો ગતિમાં હશે (વર્તુળો કે જેની સાથે અન્ય બિંદુઓ ખસે છે, સ્પર્શ કરતા નથી, પરંતુ છેદાય છે). POPў એ ગોળાના પરિભ્રમણની અક્ષ છે, જેમ કે સમયની દરેક ક્ષણે રસ્તા પર ફરતું વ્હીલ તેના સૌથી નીચલા બિંદુ પર ફરે છે. ગોળાની કોણીય વેગ શું છે? સરળતા માટે, અમે બિંદુ A પસંદ કરીએ છીએ. જેના પર અક્ષ w1 સપાટીને છેદે છે. જે સમયે આપણે વિચારી રહ્યા છીએ તે સમયે, તે અંતરે Dt સમયસર આગળ વધે છે

ત્રિજ્યાના વર્તુળની આસપાસ r sin w1. વ્યાખ્યા દ્વારા, કોણીય વેગ

આ સૂત્ર અને સંબંધ (1), આપણે મેળવીએ છીએ

બીજા શબ્દોમાં કહીએ તો, જો તમે સંખ્યાત્મક મૂલ્ય લખો છો અને ઉપર વર્ણવ્યા મુજબ કોણીય વેગની દિશા પસંદ કરો છો, તો આ જથ્થાઓને વેક્ટર તરીકે ઉમેરવામાં આવે છે અને તે જેમ ગણી શકાય. તમે હવે ક્રોસ ઉત્પાદન દાખલ કરી શકો છો; કોણીય વેગ w સાથે ફરતા શરીરને ધ્યાનમાં લો. ચાલો શરીર પરના કોઈપણ બિંદુ P અને કોઓર્ડિનેટ્સ O ના કોઈપણ મૂળને પસંદ કરીએ, જે પરિભ્રમણની અક્ષ પર સ્થિત છે. ચાલો r એ O થી P તરફ નિર્દેશિત વેક્ટર હોઈએ. બિંદુ P એક વર્તુળમાં V = w r sin (w, r) ગતિ સાથે ફરે છે. વેગ વેક્ટર V વર્તુળની સ્પર્શક છે અને ફિગમાં બતાવેલ દિશામાં નિર્દેશ કરે છે. આઠ

ચાલો જોઈએ કે ઘટકો અને એકમ વેક્ટરના સંદર્ભમાં ક્રોસ પ્રોડક્ટ કેવી રીતે લખાય છે. સૌ પ્રથમ, કોઈપણ વેક્ટર A, A * A = AA sin 0 = 0 માટે.
તેથી, એકમ વેક્ટરના કિસ્સામાં, i * i = j * j = k * k = 0 અને i * j = k, j * k = i, k * i = j. પછી,

આ સમાનતાને નિર્ણાયક તરીકે પણ લખી શકાય છે:

જો A * B = 0, તો ક્યાં તો A અથવા B 0 છે, અથવા A અને B સમરેખા છે. આમ, ડોટ પ્રોડક્ટના કિસ્સામાં, વેક્ટર દ્વારા વિભાજન શક્ય નથી. મૂલ્ય A * B એ બાજુઓ A અને B સાથેના સમાંતરગ્રામના ક્ષેત્રફળ જેટલું છે. તે જોવાનું સરળ છે, કારણ કે B sin bA, Bc તેની ઊંચાઈ છે અને A તેનો આધાર છે. અન્ય ઘણા ભૌતિક જથ્થાઓ છે જે વેક્ટર ઉત્પાદનો છે. ઇલેક્ટ્રોમેગ્નેટિઝમના સિદ્ધાંતમાં સૌથી મહત્વપૂર્ણ વેક્ટર ઉત્પાદનોમાંનું એક દેખાય છે અને તેને પોઇટિંગ વેક્ટર પી કહેવામાં આવે છે. આ વેક્ટર નીચે પ્રમાણે આપવામાં આવે છે: P = E * H, જ્યાં E અને H અનુક્રમે ઇલેક્ટ્રિક અને ચુંબકીય ક્ષેત્રોના વેક્ટર છે. વેક્ટર P ને કોઈપણ બિંદુએ ચોરસ મીટર દીઠ વોટમાં ઊર્જાના આપેલ પ્રવાહ તરીકે વિચારી શકાય છે. અહીં કેટલાક વધુ ઉદાહરણો છે: એક બિંદુ પર કામ કરતા કોઓર્ડિનેટ્સની ઉત્પત્તિ સાથે સંબંધિત ફોર ફોર ફોર્સ (ટોર્ક) જેની ત્રિજ્યા વેક્ટર r એ r * F તરીકે વ્યાખ્યાયિત થયેલ છે; દળ m અને ઝડપ V સાથે બિંદુ r પર સ્થિત એક કણ, મૂળની તુલનામાં કોણીય વેગ mr * V ધરાવે છે; ચુંબકીય ક્ષેત્ર B મારફતે ઈલેક્ટ્રિક ચાર્જ q વહન કરતા કણ પર કામ કરતું બળ V ની ઝડપ સાથે qV * B છે.
ત્રિવિધ કામ કરે છે.ત્રણ વેક્ટરમાંથી, આપણે નીચેના ટ્રિપલ પ્રોડક્ટ્સ બનાવી શકીએ છીએ: વેક્ટર (A * B) * C; વેક્ટર (A * B) * C; સ્કેલર (A * B) * C. પ્રથમ પ્રકાર વેક્ટર C અને સ્કેલર A * B નું ઉત્પાદન છે; અમે પહેલાથી જ આવા કાર્યો વિશે વાત કરી છે. બીજા પ્રકારને ડબલ વેક્ટર ઉત્પાદન કહેવામાં આવે છે; વેક્ટર A * B પ્લેન પર લંબ છે જ્યાં A અને B આવેલું છે, અને તેથી (A * B) * C એ પ્લેન A અને Bમાં પડેલું વેક્ટર છે અને C પર લંબ છે. તેથી, સામાન્ય રીતે, (A * B) * C એ A * (B * C) ની બરાબર નથી. A, B અને C ને x, y અને z અક્ષો સાથે તેમના કોઓર્ડિનેટ્સ (ઘટકો) ના સંદર્ભમાં લખીને અને ગુણાકાર કરીને, તમે બતાવી શકો છો કે A * (B * C) = B * (A * C) - C * (A * બી). ત્રીજો પ્રકારનું ઉત્પાદન, જે ઘન અવસ્થાના ભૌતિકશાસ્ત્રમાં જાળીની ગણતરી કરતી વખતે ઉદ્ભવે છે, તે સંખ્યાત્મક રીતે ધાર A, B, C સાથેના સમાંતર પાઇપના જથ્થાની બરાબર છે. ત્યારથી (A * B) * C = A * (B * C) , સ્કેલર અને વેક્ટર ગુણાકારના ચિહ્નો અદલાબદલી થઈ શકે છે, અને ભાગ ઘણીવાર (ABC) તરીકે લખવામાં આવે છે. આ ઉત્પાદન નિર્ણાયક સમાન છે

નોંધ કરો કે (A B C) = 0 જો ત્રણેય વેક્ટર એક જ પ્લેનમાં હોય અથવા જો A = 0 અથવા (અને) B = 0 અથવા (અને) C = 0 હોય.
વેક્ટરનો ભિન્નતા
ધારો કે વેક્ટર U એ એક સ્કેલર ચલ t નું કાર્ય છે. ઉદાહરણ તરીકે, U એ મૂળથી મૂવિંગ પોઈન્ટ તરફ દોરવામાં આવેલ ત્રિજ્યા વેક્ટર હોઈ શકે છે અને t સમય હોઈ શકે છે. ચાલો ટીને નાની રકમ Dt થી બદલો, જે DU દ્વારા U માં ફેરફાર તરફ દોરી જશે. આ ફિગમાં બતાવવામાં આવ્યું છે. 9. DU/Dt ગુણોત્તર એ DU ની સમાન દિશામાં નિર્દેશિત વેક્ટર છે. અમે ટી ના સંદર્ભમાં U ના વ્યુત્પન્નને વ્યાખ્યાયિત કરી શકીએ છીએ

પૂરી પાડવામાં આવેલ છે કે આવી મર્યાદા અસ્તિત્વમાં છે. બીજી બાજુ, તમે ત્રણ અક્ષો સાથેના ઘટકોના સરવાળા તરીકે U ને રજૂ કરી શકો છો અને લખી શકો છો

જો U એ ત્રિજ્યા વેક્ટર r છે, તો dr/dt એ બિંદુનો વેગ છે, જે સમયના કાર્ય તરીકે વ્યક્ત થાય છે. સમયને ફરીથી અલગ કરીને, આપણને પ્રવેગ મળે છે. ધારો કે એક બિંદુ ફિગમાં બતાવેલ વળાંક સાથે ખસે છે. 10. ચાલો વળાંક સાથે એક બિંદુ દ્વારા મુસાફરી કરેલ અંતર બનીએ. નાના સમય અંતરાલ Dt દરમિયાન, બિંદુ વળાંક સાથે અંતર Ds આવરી લેશે; ત્રિજ્યા વેક્ટરની સ્થિતિ ડૉ. આથી Dr/Ds એ ડૉ.ની જેમ નિર્દેશિત વેક્ટર છે. આગળ

વળાંક માટે એકમ વેક્ટર સ્પર્શક છે. આ હકીકત પરથી જોઈ શકાય છે કે બિંદુ Q બિંદુ P ની નજીક આવે છે, PQ સ્પર્શકની નજીક આવે છે અને Dr Ds ની નજીક આવે છે. ઉત્પાદનને અલગ પાડવા માટેના સૂત્રો એ સ્કેલર ફંક્શન્સના ઉત્પાદનને અલગ પાડવા માટેના સૂત્રો સમાન છે; જો કે, ક્રોસ ઉત્પાદન પ્રતિકૂળ હોવાથી, ગુણાકારનો ક્રમ સાચવવો જોઈએ. તેથી,

આમ, આપણે જોઈએ છીએ કે જો વેક્ટર એક સ્કેલર વેરીએબલનું ફંક્શન છે, તો આપણે ડેરિવેટિવને તે જ રીતે રજૂ કરી શકીએ છીએ જેમ કે સ્કેલર ફંક્શનના કિસ્સામાં.
વેક્ટર અને સ્કેલર ક્ષેત્રો. ઢાળ.ભૌતિકશાસ્ત્રમાં, તમારે ઘણીવાર વેક્ટર અથવા સ્કેલર જથ્થાઓ સાથે વ્યવહાર કરવો પડે છે જે આપેલ ક્ષેત્રમાં બિંદુથી બિંદુ સુધી બદલાય છે. આવા વિસ્તારોને "ક્ષેત્રો" કહેવામાં આવે છે. ઉદાહરણ તરીકે, સ્કેલર તાપમાન અથવા દબાણ હોઈ શકે છે; વેક્ટર એ ફરતા પ્રવાહીની ગતિ અથવા ચાર્જની સિસ્ટમનું ઇલેક્ટ્રોસ્ટેટિક ક્ષેત્ર હોઈ શકે છે. જો આપણે અમુક સંકલન પ્રણાલી પસંદ કરી હોય, તો આપેલ વિસ્તારમાં કોઈપણ બિંદુ P (x, y, z) અમુક ત્રિજ્યા વેક્ટર r (= xi + yj + zk) ને અનુલક્ષે છે અને વેક્ટર જથ્થાના મૂલ્ય U (r) અથવા તેની સાથે સંકળાયેલ scalar f(r) ધારો કે યુ અને એફ ડોમેનમાં વિશિષ્ટ રીતે વ્યાખ્યાયિત થયેલ છે; તે દરેક બિંદુ U અથવા f ના એક અને માત્ર એક મૂલ્યને અનુલક્ષે છે, જોકે વિવિધ બિંદુઓ, અલબત્ત, અલગ અલગ મૂલ્યો ધરાવી શકે છે. ચાલો કહીએ કે આપણે આ વિસ્તારની આસપાસ ફરતા સમયે U અને f જે ઝડપે બદલાય છે તેનું વર્ણન કરવા માંગીએ છીએ. સરળ આંશિક ડેરિવેટિવ્ઝ જેમ કે dU/dx અને df/dy અમને અનુકૂળ નથી, કારણ કે તેઓ પસંદ કરેલા ચોક્કસ સંકલન અક્ષો પર આધાર રાખે છે. જો કે, સંકલન અક્ષોની પસંદગીથી સ્વતંત્ર, વેક્ટર ડિફરન્સિયલ ઓપરેટરને રજૂ કરવું શક્ય છે; આ ઓપરેટરને "ગ્રેડિયન્ટ" કહેવામાં આવે છે. ધારો કે આપણે સ્કેલર ફીલ્ડ f સાથે કામ કરી રહ્યા છીએ. પ્રથમ, ઉદાહરણ તરીકે દેશના વિસ્તારના રૂપરેખા નકશાને ધ્યાનમાં લો. આ કિસ્સામાં f સમુદ્ર સપાટીથી ઊંચાઈ છે; સમોચ્ચ રેખાઓ સમાન f મૂલ્ય સાથે બિંદુઓને જોડે છે. આમાંની કોઈપણ રેખાઓ સાથે આગળ વધતી વખતે, f બદલાતું નથી; જો આપણે આ રેખાઓ પર કાટખૂણે ખસેડીએ, તો f ના ફેરફારનો દર મહત્તમ હશે. અમે દરેક બિંદુને વેક્ટર સાથે સાંકળી શકીએ છીએ જે ઝડપ f માં મહત્તમ ફેરફારની તીવ્રતા અને દિશા દર્શાવે છે; આવો નકશો અને આમાંના કેટલાક વેક્ટર ફિગમાં બતાવવામાં આવ્યા છે. 11. જો આપણે આ ક્ષેત્રના દરેક બિંદુ માટે કરીએ છીએ, તો આપણને સ્કેલર ક્ષેત્ર f સાથે સંકળાયેલ વેક્ટર ક્ષેત્ર મળે છે. આ "ગ્રેડિયન્ટ" f તરીકે ઓળખાતા વેક્ટરનું ક્ષેત્ર છે, જે grad f અથવા Cf (C ચિહ્નને "nabla" પણ કહેવાય છે) તરીકે લખવામાં આવે છે.

જ્યાં બિંદુઓ ઉચ્ચ ઓર્ડરની શરતો દર્શાવે છે. આ અભિવ્યક્તિ ડોટ પ્રોડક્ટ તરીકે લખી શકાય છે

અમે આ સમાનતાની જમણી અને ડાબી બાજુઓને Ds દ્વારા વિભાજીત કરીએ છીએ, અને Ds ને શૂન્ય થવા દો; પછી

જ્યાં dr/ds એ પસંદ કરેલી દિશામાં એકમ વેક્ટર છે. કૌંસમાં અભિવ્યક્તિ પસંદ કરેલ બિંદુ પર આધાર રાખીને વેક્ટર છે. આમ, df/ds નું મહત્તમ મૂલ્ય છે, જ્યારે dr/ds એ જ દિશામાં નિર્દેશ કરે છે, ત્યારે કૌંસમાં અભિવ્યક્તિ એ ઢાળ છે. આ રીતે,

- પરિમાણમાં સમાન અને કોઓર્ડિનેટ્સની તુલનામાં f ના ફેરફારના મહત્તમ દર સાથે દિશામાં એકરુપ વેક્ટર. ઢાળ f ઘણીવાર આ રીતે લખવામાં આવે છે

આનો અર્થ એ છે કે ઓપરેટર C તેના પોતાના પર અસ્તિત્વ ધરાવે છે. ઘણા કિસ્સાઓમાં તે વેક્ટરની જેમ વર્તે છે અને હકીકતમાં તે "વેક્ટર ડિફરન્સિયલ ઓપરેટર" છે - ભૌતિકશાસ્ત્રમાં સૌથી મહત્વપૂર્ણ વિભેદક ઓપરેટરોમાંનું એક. С માં એકમ વેક્ટર i, j અને k હોવા છતાં, તેનો ભૌતિક અર્થ પસંદ કરેલ કોઓર્ડિનેટ સિસ્ટમ પર આધારિત નથી. Cf અને f વચ્ચે શું સંબંધ છે? સૌ પ્રથમ, ધારો કે f કોઈપણ બિંદુએ સંભવિત નક્કી કરે છે. કોઈપણ નાના વિસ્થાપન ડૉ માટે, f ની કિંમત દ્વારા બદલાશે

જો q એક માત્રા છે (ઉદાહરણ તરીકે, સમૂહ, ચાર્જ) ડૉ પર ખસેડવામાં આવે છે, તો પછી q ને ડૉ પર ખસેડીને કરવામાં આવેલ કાર્ય બરાબર છે

ત્યારથી ડૉ - વિસ્થાપન, પછી qСf - બળ; -Cf - f સાથે સંકળાયેલ તણાવ (જથ્થાના એકમ દીઠ બળ). ઉદાહરણ તરીકે, ચાલો U એ ઇલેક્ટ્રોસ્ટેટિક સંભવિત બનીએ; પછી E એ વિદ્યુત ક્ષેત્રની તાકાત છે, જે સૂત્ર E = -CU દ્વારા આપવામાં આવે છે. ચાલો ધારીએ કે U એ મૂળ સ્થાને મૂકવામાં આવેલ q કૂલમ્બમાં વિદ્યુત ચાર્જ બિંદુ દ્વારા બનાવવામાં આવ્યું છે. ત્રિજ્યા વેક્ટર r સાથે બિંદુ P (x, y, z) પર U મૂલ્ય સૂત્ર દ્વારા આપવામાં આવે છે

જ્યાં e0 એ ખાલી જગ્યાનો ડાઇલેક્ટ્રિક સ્થિરાંક છે. તેથી

જ્યાંથી તે અનુસરે છે કે E એ r દિશામાં કાર્ય કરે છે અને તેનું મૂલ્ય q / (4pe0r3) છે. સ્કેલર ફીલ્ડને જાણીને, તમે સંકળાયેલ વેક્ટર ફીલ્ડ નક્કી કરી શકો છો. વિપરીત પણ શક્ય છે. ગાણિતિક પ્રક્રિયાના દૃષ્ટિકોણથી, સ્કેલર ક્ષેત્રો વેક્ટર કરતા વધુ સરળ છે, કારણ કે તે એક સંકલન કાર્ય દ્વારા નિર્દિષ્ટ કરવામાં આવે છે, જ્યારે વેક્ટર ક્ષેત્રને ત્રણ કાર્યોની જરૂર હોય છે, જે ત્રણ દિશામાં વેક્ટરના ઘટકોને અનુરૂપ હોય છે. આમ, પ્રશ્ન ઊભો થાય છે: વેક્ટર ક્ષેત્ર આપવામાં આવે છે, શું આપણે સંકળાયેલ સ્કેલર ક્ષેત્ર લખી શકીએ?
ડાયવર્જન્સ અને રોટર.અમે સ્કેલર ફંક્શન પર કામ કરતા Cનું પરિણામ જોયું છે. જો વેક્ટર પર C લાગુ કરવામાં આવે તો શું થશે? ત્યાં બે શક્યતાઓ છે: U (x, y, z) ને વેક્ટર બનવા દો; પછી આપણે નીચે પ્રમાણે વેક્ટર અને સ્કેલર પ્રોડક્ટ્સ બનાવી શકીએ છીએ:

આમાંની પ્રથમ અભિવ્યક્તિ એક સ્કેલર છે જેને ડાયવર્જન્સ U (divU દ્વારા સૂચવવામાં આવે છે); બીજો એક વેક્ટર છે જેને રોટર U (rotU દ્વારા સૂચિત) કહેવાય છે. આ વિભેદક કાર્યો, વિચલન અને રોટર, ગાણિતિક ભૌતિકશાસ્ત્રમાં વ્યાપકપણે ઉપયોગમાં લેવાય છે. કલ્પના કરો કે U એ અમુક વેક્ટર છે અને તે અને તેના પ્રથમ ડેરિવેટિવ્સ અમુક પ્રદેશમાં સતત છે. ચાલો P આ પ્રદેશમાં એક બિંદુ હોઈએ જે નાની બંધ સપાટી S થી ઘેરાયેલો છે જે વોલ્યુમ DV ને બંધ કરે છે. ચાલો n દરેક બિંદુએ આ સપાટી પર લંબરૂપ એકમ વેક્ટર હોઈએ (સપાટીની આસપાસ ફરતી વખતે n દિશા બદલે છે, પરંતુ હંમેશા એકમ લંબાઈ ધરાવે છે); બહારની તરફ નિર્દેશ કરવા દો. ચાલો તે બતાવીએ

અહીં S સૂચવે છે કે આ પૂર્ણાંકો સમગ્ર સપાટી પર લેવામાં આવ્યા છે, da એ સપાટી Sનું એક તત્વ છે. સરળતા માટે, અમે Dx બાજુઓ સાથે નાના સમાંતર (ફિગ. 12 માં બતાવ્યા પ્રમાણે) ના સ્વરૂપમાં અનુકૂળ આકાર S પસંદ કરીશું. , Dy અને Dz; બિંદુ P એ સમાંતર નળીઓનું કેન્દ્ર છે. ચાલો પહેલા સમીકરણ (4) માંથી સમાંતર ના એક ચહેરા સાથે અવિભાજ્યની ગણતરી કરીએ. આગળના ચહેરા માટે n = i (એકમ વેક્ટર x-અક્ષની સમાંતર છે); ડા = DyDz. સામેના ચહેરા પરથી અભિન્નનો ફાળો છે

વિરુદ્ધ બાજુ પર n = -i; આ ચહેરો અભિન્નતામાં ફાળો આપે છે

ટેલરના પ્રમેયનો ઉપયોગ કરીને, અમે બે ચહેરાઓમાંથી કુલ યોગદાન મેળવીએ છીએ

નોંધ કરો કે DxDyDz = DV. એ જ રીતે, તમે ચહેરાની અન્ય બે જોડીમાંથી યોગદાનની ગણતરી કરી શકો છો. સંપૂર્ણ અભિન્ન છે

અને જો આપણે DV (r) 0 મૂકીએ, તો ઉચ્ચ ઓર્ડરની શરતો અદૃશ્ય થઈ જાય છે. સૂત્ર (2) મુજબ, કૌંસમાં અભિવ્યક્તિ divU છે, જે સમાનતા (4) સાબિત કરે છે. સમાનતા (5) એ જ રીતે સાબિત કરી શકાય છે. ચાલો ફરી ફિગનો ઉપયોગ કરીએ. 12; પછી આગળના ચહેરાથી અવિભાજ્યમાં યોગદાન સમાન હશે

અને, ટેલરના પ્રમેયનો ઉપયોગ કરીને, અમે શોધી કાઢ્યું છે કે બે ચહેરાઓમાંથી અવિભાજ્યમાં કુલ યોગદાનનું સ્વરૂપ છે

તે સમીકરણ (3) માં rotU માટેની અભિવ્યક્તિમાંથી આ બે શબ્દો છે. બાકીની ચાર શરતો અન્ય ચાર ચહેરાઓના યોગદાનને ધ્યાનમાં લીધા પછી મેળવવામાં આવશે. સારમાં, આ ગુણોત્તરનો અર્થ શું છે? સમાનતાનો વિચાર કરો (4). ધારો કે U એ વેગ છે (ઉદાહરણ તરીકે, પ્રવાહીની). પછી nЧU da = Un da, જ્યાં Un એ વેક્ટર U નો સપાટી પરનો સામાન્ય ઘટક છે. તેથી, Un da ​​એ સમયના એકમ દીઠ da દ્વારા વહેતા પ્રવાહીનું પ્રમાણ છે, અને સમયના એકમ દીઠ S દ્વારા વહેતા પ્રવાહીનું પ્રમાણ છે. આથી,

બિંદુ P ની આસપાસ વોલ્યુમના એકમના વિસ્તરણનો દર. તેથી વિચલનને તેનું નામ મળ્યું; તે ઝડપ દર્શાવે છે કે જેની સાથે પ્રવાહી P થી વિસ્તરે છે (એટલે ​​કે થી અલગ પડે છે) પ્લેન-સમાંતર સપાટીઓ અમે પસંદ કરીએ છીએ તે કોઈપણ દિશામાં લક્ષી હોઈ શકે છે. k ને દરેક સપાટી પર લંબરૂપ એકમ વેક્ટર ગણવા દો, અને દરેક સપાટી DA નો વિસ્તાર દો; પછી કુલ વોલ્યુમ DV = hDA (ફિગ. 13). હવે અભિન્ન ધ્યાનમાં લો

સ્વતંત્ર ઉકેલ માટેના કાર્યો પણ હશે, જેના તમે જવાબો જોઈ શકશો.

વેક્ટર ખ્યાલ

તમે વેક્ટર્સ અને તેના પરના ઑપરેશન વિશે બધું શીખો તે પહેલાં, એક સરળ સમસ્યાને ઉકેલવા માટે ટ્યુન ઇન કરો. તમારી સાહસિકતાનું એક વેક્ટર છે અને તમારી નવીન ક્ષમતાઓનું વેક્ટર છે. સાહસિકતાનું વેક્ટર તમને ધ્યેય 1 તરફ લઈ જાય છે, અને નવીન ક્ષમતાઓનું વેક્ટર લક્ષ્ય 2 તરફ લઈ જાય છે. રમતના નિયમો એવા છે કે તમે એક સાથે આ બે વેક્ટરની દિશામાં આગળ વધી શકતા નથી અને એક સાથે બે લક્ષ્યો હાંસલ કરી શકતા નથી. વેક્ટર્સ ક્રિયાપ્રતિક્રિયા કરે છે, અથવા, ગાણિતિક દ્રષ્ટિએ, વેક્ટર પર કેટલીક કામગીરી કરવામાં આવે છે. આ ઓપરેશનનું પરિણામ "પરિણામ" વેક્ટર છે, જે તમને લક્ષ્ય 3 તરફ દોરી જાય છે.

હવે મને કહો: "એન્ટરપ્રાઇઝ" અને "ઇનોવેટિવ એબિલિટી" વેક્ટર પરના કયા ઓપરેશનનું પરિણામ વેક્ટર "પરિણામ" છે? જો તમે તરત જ કહી શકતા નથી, તો નિરાશ થશો નહીં. જેમ જેમ તમે આ પાઠમાંથી આગળ વધશો તેમ, તમે આ પ્રશ્નનો જવાબ આપવા માટે સમર્થ હશો.

આપણે ઉપર જોયું તેમ, વેક્ટર આવશ્યકપણે અમુક બિંદુથી જાય છે એઅમુક બિંદુ સુધી સીધી રેખામાં બી... તેથી, દરેક વેક્ટરમાં માત્ર સંખ્યાત્મક મૂલ્ય નથી - લંબાઈ, પણ ભૌતિક અને ભૌમિતિક - દિશાનિર્દેશકતા. આ વેક્ટરની પ્રથમ અને સરળ વ્યાખ્યા તરફ દોરી જાય છે. તેથી, વેક્ટર એ બિંદુ પરથી જતો નિર્દેશિત સેગમેન્ટ છે એસીધા મુદ્દા પર બી... તે નીચે પ્રમાણે નિયુક્ત થયેલ છે:.

અને અલગ શરૂ કરવા માટે વેક્ટર કામગીરી , આપણે વધુ એક વેક્ટર વ્યાખ્યાથી પરિચિત થવાની જરૂર છે.

વેક્ટર એ બિંદુનું એક પ્રકારનું પ્રતિનિધિત્વ છે કે જ્યાં તમે કોઈ પ્રારંભિક બિંદુથી મેળવવા માંગો છો. ઉદાહરણ તરીકે, ત્રિ-પરિમાણીય વેક્ટર સામાન્ય રીતે લખવામાં આવે છે (x, y, z) . તદ્દન સરળ રીતે, આ સંખ્યાઓ દર્શાવે છે કે એક બિંદુ સુધી પહોંચવા માટે ત્રણ અલગ-અલગ દિશામાં મુસાફરી કરવી કેટલી દૂર છે.

એક વેક્ટર આપવા દો. જેમાં x = 3 (જમણો હાથ જમણી તરફ નિર્દેશ કરે છે) y = 1 (ડાબા હાથ આગળ પોઈન્ટ કરે છે) z = 5 (બિંદુની નીચે એક સીડી છે જે ઉપર જાય છે). આ માહિતી અનુસાર, તમે જમણા હાથ દ્વારા દર્શાવેલ દિશામાં 3 મીટર ચાલવાથી એક બિંદુ મેળવશો, પછી ડાબા હાથ દ્વારા દર્શાવેલ દિશામાં 1 મીટર, અને પછી એક સીડી તમારી રાહ જોશે અને, 5 મીટર ચડતા, તમે આખરે આ જશો. તમારી જાતને અંતિમ બિંદુ પર શોધો.

અન્ય તમામ શરતો ઉપરોક્ત સમજૂતીની શુદ્ધિકરણ છે, જે વેક્ટર્સ પરની વિવિધ કામગીરી માટે જરૂરી છે, એટલે કે વ્યવહારિક સમસ્યાઓ ઉકેલવા માટે. ચાલો આ કડક વ્યાખ્યાઓમાંથી પસાર થઈએ, લાક્ષણિક વેક્ટર સમસ્યાઓ પર ધ્યાન આપીએ.

ભૌતિક ઉદાહરણોવેક્ટર જથ્થાઓ અવકાશમાં ફરતા પદાર્થના બિંદુનું વિસ્થાપન, આ બિંદુની ગતિ અને પ્રવેગક તેમજ તેના પર કાર્ય કરતું બળ હોઈ શકે છે.

ભૌમિતિક વેક્ટરફોર્મમાં દ્વિ-પરિમાણીય અને ત્રિ-પરિમાણીય અવકાશમાં પ્રસ્તુત દિશાત્મક સેગમેન્ટ... આ એક સેગમેન્ટ છે, જે શરૂઆત અને અંત વચ્ચેનો તફાવત દર્શાવે છે.

જો એવેક્ટરની શરૂઆત છે, અને બી- તેનો અંત, પછી વેક્ટરને પ્રતીક અથવા એક લોઅરકેસ અક્ષર દ્વારા સૂચવવામાં આવે છે. આકૃતિમાં, વેક્ટરનો છેડો તીર દ્વારા દર્શાવવામાં આવ્યો છે (ફિગ. 1)

લંબાઈ(અથવા મોડ્યુલભૌમિતિક વેક્ટરનું ) તે પેદા કરતા સેગમેન્ટની લંબાઈ છે

બે વેક્ટર કહેવાય છે સમાન , જો તેઓ સમાંતર સ્થાનાંતરણના માધ્યમથી સંરેખિત થઈ શકે (જો દિશાઓ એકરૂપ હોય તો), એટલે કે. જો તેઓ સમાંતર હોય, તો સમાન દિશામાં નિર્દેશ કરો અને તેમની લંબાઈ સમાન હોય.

ભૌતિકશાસ્ત્રમાં, તે ઘણીવાર ગણવામાં આવે છે એન્કર કરેલ વેક્ટરએપ્લિકેશનના બિંદુ, લંબાઈ અને દિશા દ્વારા આપવામાં આવે છે. જો વેક્ટરના ઉપયોગના બિંદુથી કોઈ ફરક પડતો નથી, તો તેને સ્થાનાંતરિત કરી શકાય છે, અવકાશના કોઈપણ બિંદુ સુધી લંબાઈ અને દિશા જાળવી રાખી શકાય છે. આ કિસ્સામાં, વેક્ટર કહેવામાં આવે છે મફત... અમે ફક્ત ધ્યાનમાં લેવા સંમત થઈશું મફત વેક્ટર.

ભૌમિતિક વેક્ટર પર રેખીય કામગીરી

સંખ્યા વડે વેક્ટરનો ગુણાકાર

વેક્ટરનું ઉત્પાદન નંબર દ્વારાવેક્ટરને સ્ટ્રેચિંગ (એટ) અથવા કમ્પ્રેશન (એટ) દ્વારા વેક્ટરમાંથી મેળવેલ વેક્ટર કહેવાય છે, અને વેક્ટરની દિશા સચવાય છે, જો, અને વિરુદ્ધમાં બદલાય છે, જો. (ફિગ. 2)

તે વ્યાખ્યામાંથી અનુસરે છે કે વેક્ટર અને = હંમેશા એક અથવા સમાંતર રેખાઓ પર સ્થિત હોય છે. આવા વેક્ટર કહેવામાં આવે છે સમરેખા... (તમે એમ પણ કહી શકો કે આ વેક્ટર્સ સમાંતર છે, પરંતુ વેક્ટર બીજગણિતમાં "કોલિનિયર" કહેવાનો રિવાજ છે.) આ વાત પણ સાચી છે: જો વેક્ટર અને કોલિનિયર છે, તો તે સંબંધ દ્વારા સંબંધિત છે.

તેથી, સમાનતા (1) બે વેક્ટર માટે સમન્વય સ્થિતિને વ્યક્ત કરે છે.

વેક્ટરનો સરવાળો અને બાદબાકી

વેક્ટર ઉમેરતી વખતે, તમારે તે જાણવાની જરૂર છે સરવાળોવેક્ટર અને તેને વેક્ટર કહેવામાં આવે છે, જેની શરૂઆત વેક્ટરની શરૂઆત સાથે એકરુપ હોય છે, અને અંત - વેક્ટરના અંત સાથે, જો કે વેક્ટરની શરૂઆત વેક્ટરના અંત સાથે જોડાયેલ હોય. (ફિગ. 3)

આ વ્યાખ્યા કોઈપણ મર્યાદિત સંખ્યામાં વેક્ટર્સ પર વિતરિત કરી શકાય છે. જગ્યા આપવા દો nમફત વેક્ટર. ઘણા વેક્ટર ઉમેરતી વખતે, બંધ વેક્ટર તેમના સરવાળા તરીકે લેવામાં આવે છે, જેની શરૂઆત પ્રથમ વેક્ટરની શરૂઆત સાથે એકરુપ હોય છે, અને અંત - છેલ્લા વેક્ટરના અંત સાથે. એટલે કે, જો તમે વેક્ટરની શરૂઆતને વેક્ટરના અંત સાથે અને વેક્ટરની શરૂઆતને વેક્ટરના અંત સાથે જોડો છો, વગેરે. અને, છેવટે, વેક્ટરના અંત સુધી - વેક્ટરની શરૂઆત, પછી આ વેક્ટરનો સરવાળો બંધ વેક્ટર છે જેની શરૂઆત પ્રથમ વેક્ટરની શરૂઆત સાથે થાય છે, અને અંત - છેલ્લા વેક્ટરના અંત સાથે. (ફિગ. 4)

શરતોને વેક્ટરના ઘટકો કહેવામાં આવે છે, અને ઘડાયેલ નિયમ છે બહુકોણ નિયમ... આ બહુકોણ સપાટ ન હોઈ શકે.

જ્યારે તમે વેક્ટરને -1 વડે ગુણાકાર કરો છો, ત્યારે તમને વિરુદ્ધ વેક્ટર મળે છે. વેક્ટર અને સમાન લંબાઈ અને વિરુદ્ધ દિશાઓ ધરાવે છે. તેમની રકમ આપે છે શૂન્ય વેક્ટરજેની લંબાઈ શૂન્ય છે. શૂન્ય વેક્ટરની દિશા અવ્યાખ્યાયિત છે.

વેક્ટર બીજગણિતમાં, બાદબાકીની કામગીરીને અલગથી ધ્યાનમાં લેવાની જરૂર નથી: વેક્ટરમાંથી વેક્ટરને બાદ કરવાનો અર્થ થાય છે કે વિરુદ્ધ વેક્ટરને વેક્ટરમાં ઉમેરવું, એટલે કે.

ઉદાહરણ 1.અભિવ્યક્તિને સરળ બનાવો:

.

,

એટલે કે, બહુપદી (ખાસ કરીને, અભિવ્યક્તિને સરળ બનાવવાના કાર્યો પણ) ની જેમ વેક્ટરને સંખ્યાઓ દ્વારા ઉમેરી અને ગુણાકાર કરી શકાય છે. સામાન્ય રીતે, વેક્ટરના ઉત્પાદનોની ગણતરી કરતા પહેલા વેક્ટર સાથે રેખીય સમાન અભિવ્યક્તિઓને સરળ બનાવવાની જરૂરિયાત ઊભી થાય છે.

ઉદાહરણ 2.વેક્ટર અને સમાંતર ABCD (ફિગ. 4a) ના કર્ણ તરીકે સેવા આપે છે. બંને વેક્ટરના સંદર્ભમાં વ્યક્ત કરો, અને, જે આ સમાંતરગ્રામની બાજુઓ છે.

ઉકેલ. સમાંતરચતુષ્કોણ કર્ણનો આંતરછેદ બિંદુ દરેક કર્ણને અડધા ભાગમાં વહેંચે છે. અમે સમસ્યા નિવેદનમાં જરૂરી વેક્ટરની લંબાઈ શોધીએ છીએ કાં તો ઇચ્છિત રાશિઓ સાથે ત્રિકોણ બનાવતા વેક્ટરના અડધા સરવાળા તરીકે, અથવા અડધા તફાવતો (વિકર્ણ તરીકે સેવા આપતા વેક્ટરની દિશા પર આધાર રાખીને), અથવા, પછીના કિસ્સામાં, બાદબાકી ચિહ્ન સાથે લેવામાં આવેલ અડધી રકમ. પરિણામ એ સમસ્યા નિવેદનમાં જરૂરી વેક્ટર છે:

આ પાઠની શરૂઆતમાં તમે આંત્રપ્રિન્યોરશિપ અને ઇનોવેટિવ એબિલિટી વેક્ટર વિશેના પ્રશ્નનો સાચો જવાબ આપ્યો છે એવું માનવાનું દરેક કારણ છે. સાચો જવાબ: આ વેક્ટર પર ઉમેરણ કામગીરી કરવામાં આવે છે.

વેક્ટર સમસ્યાઓ જાતે ઉકેલો અને પછી ઉકેલો જુઓ

વેક્ટરના સરવાળાની લંબાઈ કેવી રીતે શોધવી?

આ કાર્ય વેક્ટર કામગીરીમાં વિશિષ્ટ સ્થાન લે છે, કારણ કે તેમાં ત્રિકોણમિતિ ગુણધર્મોનો ઉપયોગ સામેલ છે. ચાલો કહીએ કે તમે નીચેના જેવા કાર્યમાં આવો છો:

વેક્ટરની લંબાઈ આપેલ છે અને આ વેક્ટરના સરવાળાની લંબાઈ. આ વેક્ટર વચ્ચેના તફાવતની લંબાઈ શોધો.

આ અને અન્ય સમાન સમસ્યાઓના ઉકેલો અને તેમને કેવી રીતે ઉકેલવા તે અંગેના ખુલાસાઓ - પાઠમાં " વેક્ટર સરવાળો: વેક્ટર સરવાળો લંબાઈ અને કોસાઈન પ્રમેય ".

અને તમે આવી સમસ્યાઓના ઉકેલને તપાસી શકો છો ઓનલાઈન કેલ્ક્યુલેટર "ત્રિકોણની અજાણી બાજુ (વેક્ટર ઉમેરણ અને કોસાઈન પ્રમેય)" .

વેક્ટરના ઉત્પાદનો ક્યાં છે?

વેક્ટર-બાય-વેક્ટર પ્રોડક્ટ્સ રેખીય કામગીરી નથી અને તેને અલગથી ગણવામાં આવે છે. અને અમારી પાસે વેક્ટર્સ અને વેક્ટરનું ડોટ પ્રોડક્ટ અને વેક્ટર ટ્યુટોરિયલ્સનું મિશ્ર ઉત્પાદન છે.

ધરી પર વેક્ટરનું પ્રક્ષેપણ

અક્ષ પર વેક્ટરનું પ્રક્ષેપણ વેક્ટર અને અક્ષ વચ્ચેના કોણના કોસાઇન દ્વારા અંદાજિત વેક્ટરની લંબાઈના ઉત્પાદન જેટલું છે:

જેમ તમે જાણો છો, બિંદુનું પ્રક્ષેપણ એસીધી રેખા પર (વિમાન) એ સીધી રેખા (વિમાન) પર આ બિંદુથી નીચે પડેલા લંબનો આધાર છે.

ચાલો એક મનસ્વી વેક્ટર હોઈએ (ફિગ. 5), અને તેની શરૂઆતના અંદાજો હોઈએ (બિંદુઓ એ) અને અંત (પોઈન્ટ બી) પ્રતિ અક્ષ l... (બિંદુનું પ્રક્ષેપણ બાંધવા માટે એ) બિંદુ દ્વારા સીધી રેખા પર એસીધી રેખા પર લંબરૂપ વિમાન. લાઇન અને પ્લેનનું આંતરછેદ જરૂરી પ્રક્ષેપણને વ્યાખ્યાયિત કરશે.

વેક્ટર ઘટક l-અક્ષ પરઆ અક્ષ પર પડેલા વેક્ટરને કહેવામાં આવે છે, જેની શરૂઆત શરૂઆતના પ્રક્ષેપણ સાથે એકરુપ હોય છે, અને અંત - વેક્ટરના અંતના પ્રક્ષેપણ સાથે.

ધરી પર વેક્ટરનું પ્રક્ષેપણ lનંબર પર ફોન કર્યો

,

આ અક્ષ પરના ઘટક વેક્ટરની લંબાઈ જેટલી, જો ઘટકોની દિશા અક્ષની દિશા સાથે એકરુપ હોય તો વત્તા ચિહ્ન સાથે લેવામાં આવે છે l, અને જો આ દિશાઓ વિરુદ્ધ હોય તો ઓછા ચિહ્ન સાથે.

ધરી પર વેક્ટર અંદાજોના મૂળભૂત ગુણધર્મો:

1. સમાન ધરી પર સમાન વેક્ટરના અંદાજો એકબીજા સાથે સમાન છે.

2. વેક્ટરને સંખ્યા વડે ગુણાકાર કરતી વખતે, તેનું પ્રક્ષેપણ સમાન સંખ્યા વડે ગુણાકાર થાય છે.

3. કોઈપણ ધરી પરના વેક્ટર્સના સરવાળાનું પ્રક્ષેપણ એ જ ધરી પરના વેક્ટરના સમન્ડના અંદાજોના સરવાળા જેટલું હોય છે.

4. અક્ષ પર વેક્ટરનું પ્રક્ષેપણ વેક્ટર અને અક્ષ વચ્ચેના કોણના કોસાઇન દ્વારા અંદાજિત વેક્ટરની લંબાઈના ઉત્પાદન જેટલું છે:

.

ઉકેલ. એક ધરી પર વેક્ટર્સ પ્રોજેક્ટ કરો lઉપરના સૈદ્ધાંતિક પૃષ્ઠભૂમિમાં વ્યાખ્યાયિત કર્યા મુજબ. ફિગ. 5a થી સ્પષ્ટ છે કે વેક્ટર્સના સરવાળાનું પ્રોજેક્શન વેક્ટરના અંદાજોના સરવાળા જેટલું છે. અમે આ અંદાજોની ગણતરી કરીએ છીએ:

વેક્ટર્સના સરવાળાનું અંતિમ પ્રક્ષેપણ શોધો:

અવકાશમાં લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ સાથે વેક્ટરનો સંબંધ

સાથે પરિચય અવકાશમાં એક લંબચોરસ કાર્ટેશિયન કોઓર્ડિનેટ સિસ્ટમ અનુરૂપ પાઠમાં થઈ હતી, તેને નવી વિન્ડોમાં ખોલવું ઇચ્છનીય છે.

આદેશિત સંકલન પ્રણાલીમાં 0xyzધરી બળદકહેવાય છે એબ્સીસા, ધરી 0y – y-અક્ષ, અને ધરી 0z – ધરી લાગુ.

મનસ્વી બિંદુ સાથે એમજગ્યા અમે વેક્ટરને સાંકળીએ છીએ

કહેવાય છે ત્રિજ્યા વેક્ટરપોઈન્ટ એમઅને તેને દરેક સંકલન અક્ષો પર પ્રક્ષેપિત કરો. ચાલો અનુરૂપ અંદાજોના મૂલ્યો સૂચવીએ:

સંખ્યાઓ x, y, zને બોલાવ્યા હતા બિંદુ M ના કોઓર્ડિનેટ્સ, અનુક્રમે એબ્સીસા, ઓર્ડિનેટઅને અરજી કરવી, અને સંખ્યાઓના ક્રમબદ્ધ બિંદુ તરીકે લખવામાં આવે છે: M (x; y; z)(ફિગ. 6).

એકમ લંબાઈનો વેક્ટર, જેની દિશા ધરીની દિશા સાથે મેળ ખાય છે, તેને કહેવામાં આવે છે એકમ વેક્ટર(અથવા ઓર્થોમ) અક્ષ. ચાલો દ્વારા સૂચિત કરીએ

તદનુસાર, સંકલન અક્ષોના એકમ વેક્ટર બળદ, ઓય, ઓઝ

પ્રમેય.કોઈપણ વેક્ટરને સંકલન અક્ષોના એકમ વેક્ટર સાથે વિસ્તૃત કરી શકાય છે:

(2)

સમાનતા (2) ને સંકલન અક્ષો સાથે વેક્ટરનું વિસ્તરણ કહેવામાં આવે છે. આ વિસ્તરણના ગુણાંક એ સંકલન અક્ષો પરના વેક્ટરના અંદાજો છે. આમ, સંકલન અક્ષો સાથે વેક્ટરના વિસ્તરણના ગુણાંક (2) એ વેક્ટરના કોઓર્ડિનેટ્સ છે.

અવકાશમાં ચોક્કસ કોઓર્ડિનેટ સિસ્ટમ પસંદ કર્યા પછી, વેક્ટર અને તેના કોઓર્ડિનેટ્સનો ત્રિપુટી એકબીજાને વિશિષ્ટ રીતે નિર્ધારિત કરે છે, તેથી વેક્ટરને ફોર્મમાં લખી શકાય છે.

(2) અને (3) સ્વરૂપમાં વેક્ટરનું પ્રતિનિધિત્વ સમાન છે.

કોઓર્ડિનેટ્સમાં વેક્ટર્સ માટે સમકક્ષતા સ્થિતિ

જેમ આપણે પહેલેથી જ નોંધ્યું છે તેમ, વેક્ટર જો સંબંધ દ્વારા સંબંધિત હોય તો તેને કોલિનિયર કહેવામાં આવે છે

વેક્ટર્સ દો ... જો વેક્ટરના કોઓર્ડિનેટ્સ સંબંધ દ્વારા સંબંધિત હોય તો આ વેક્ટર સમરેખીય હોય છે

,

એટલે કે, વેક્ટરના કોઓર્ડિનેટ્સ પ્રમાણસર છે.

ઉદાહરણ 6.આપેલ વેક્ટર ... શું આ વેક્ટર સમરેખા છે?

ઉકેલ. ચાલો આ વેક્ટરના કોઓર્ડિનેટ્સનો ગુણોત્તર શોધીએ:

.

વેક્ટરના કોઓર્ડિનેટ્સ પ્રમાણસર હોય છે, તેથી, વેક્ટર સમરેખા હોય છે, અથવા, જે સમાન હોય છે, સમાંતર હોય છે.

વેક્ટર લંબાઈ અને દિશા કોસાઈન્સ

સંકલન અક્ષોની પરસ્પર લંબતાને કારણે, વેક્ટરની લંબાઈ

વેક્ટર પર બાંધવામાં આવેલા લંબચોરસ સમાંતરના કર્ણની લંબાઈ જેટલી છે

અને સમાનતા દ્વારા વ્યક્ત થાય છે

(4)

વેક્ટરને બે બિંદુઓ (પ્રારંભ અને અંત) નો ઉલ્લેખ કરીને સંપૂર્ણપણે વ્યાખ્યાયિત કરવામાં આવે છે, તેથી વેક્ટરના કોઓર્ડિનેટ્સ આ બિંદુઓના કોઓર્ડિનેટ્સના સંદર્ભમાં વ્યક્ત કરી શકાય છે.

ચાલો, આપેલ સંકલન પ્રણાલીમાં, વેક્ટરનું મૂળ બિંદુ પર હોવું જોઈએ

અને અંત બિંદુ પર છે

સમાનતા થી

તે અનુસરે છે

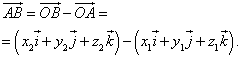
અથવા સંકલન સ્વરૂપમાં

આથી, વેક્ટરના કોઓર્ડિનેટ્સ અંત અને વેક્ટરની શરૂઆતના સમાન નામના કોઓર્ડિનેટ્સના તફાવતો સમાન છે ... આ કિસ્સામાં ફોર્મ્યુલા (4) ફોર્મ લે છે

વેક્ટરની દિશા દ્વારા નક્કી કરવામાં આવે છે દિશા કોસાઇન્સ ... આ ખૂણાઓના કોસાઇન્સ છે જે વેક્ટર અક્ષો સાથે બનાવે છે બળદ, ઓયઅને ઓઝ... ચાલો આ ખૂણાઓને અનુક્રમે સૂચિત કરીએ α , β અને γ ... પછી સૂત્રો દ્વારા આ ખૂણાઓના કોસાઈન્સ શોધી શકાય છે

વેક્ટરના ડાયરેક્શનલ કોસાઈન્સ પણ આ વેક્ટરના એકમ વેક્ટરના કોઓર્ડિનેટ્સ છે અને આમ, વેક્ટર વેક્ટર

.

ધ્યાનમાં લેતા કે વેક્ટર ઓર્ટની લંબાઈ એક એકમ જેટલી છે, એટલે કે

,

દિશા કોસાઇન્સ માટે આપણે નીચેની સમાનતા મેળવીએ છીએ:

ઉદાહરણ 7.વેક્ટરની લંબાઈ શોધો x = (3; 0; 4).

ઉકેલ. વેક્ટરની લંબાઈ છે

ઉદાહરણ 8.પોઈન્ટ આપવામાં આવે છે:

આ બિંદુઓ પર બનેલો ત્રિકોણ સમદ્વિબાજુ છે કે કેમ તે શોધો.

ઉકેલ. વેક્ટર (6) ની લંબાઈ માટેના સૂત્રનો ઉપયોગ કરીને, આપણે બાજુઓની લંબાઈ શોધીએ છીએ અને તે સ્થાપિત કરીએ છીએ કે શું તેમની વચ્ચે બે સમાન છે:

બે સમાન બાજુઓ મળી આવી હતી, તેથી ત્રીજી બાજુની લંબાઈ જોવાની જરૂર નથી, અને આપેલ ત્રિકોણ સમદ્વિબાજુ છે.

ઉદાહરણ 9.વેક્ટરની લંબાઈ અને તેની દિશા કોસાઈન્સ શોધો જો .

ઉકેલ. વેક્ટર કોઓર્ડિનેટ્સ આપવામાં આવે છે:

.

વેક્ટરની લંબાઈ વેક્ટરના કોઓર્ડિનેટ્સના ચોરસના સરવાળાના વર્ગમૂળ જેટલી છે:

.

દિશા કોસાઇન્સ શોધો:

વેક્ટર સમસ્યા જાતે ઉકેલો અને પછી ઉકેલ જુઓ

સંકલન સ્વરૂપમાં ઉલ્લેખિત વેક્ટર પરની કામગીરી

ચાલો ત્યાં બે વેક્ટર આપવામાં આવે અને, તેમના અંદાજો દ્વારા આપવામાં આવે:

ચાલો આ વેક્ટર પરની ક્રિયાઓ સૂચવીએ.

વ્યાખ્યા

વેક્ટર(lat માંથી." વેક્ટર"-" બેરિંગ") - અવકાશમાં અથવા પ્લેન પર સીધી રેખાનો નિર્દેશિત સેગમેન્ટ.

ગ્રાફિકલી રીતે, વેક્ટરને ચોક્કસ લંબાઈના નિર્દેશિત રેખાખંડ તરીકે દર્શાવવામાં આવે છે. વેક્ટર, જેની શરૂઆત એક બિંદુ પર હોય છે, અને એક બિંદુ પર અંત, તરીકે સૂચવવામાં આવે છે (ફિગ. 1). ઉપરાંત, વેક્ટરને એક નાના અક્ષરથી સૂચિત કરી શકાય છે, ઉદાહરણ તરીકે,.

જો કોઓર્ડિનેટ સિસ્ટમ અવકાશમાં નિર્દિષ્ટ કરવામાં આવી હોય, તો વેક્ટર તેના કોઓર્ડિનેટ્સના સમૂહ દ્વારા વિશિષ્ટ રીતે સ્પષ્ટ કરી શકાય છે. એટલે કે, વેક્ટરને એવા પદાર્થ તરીકે સમજવામાં આવે છે કે જેની તીવ્રતા (લંબાઈ), દિશા અને એપ્લિકેશનનો બિંદુ (વેક્ટરની શરૂઆત) હોય.

વેક્ટર કેલ્ક્યુલસની શરૂઆત 1831 માં જર્મન ગણિતશાસ્ત્રી, મિકેનિક, ભૌતિકશાસ્ત્રી, ખગોળશાસ્ત્રી અને મોજણીકર્તા જોહાન કાર્લ ફ્રેડરિક ગૌસ (1777-1855) ના કાર્યોમાં દેખાય છે. વેક્ટર્સ સાથેની કામગીરી પરના કાર્યો આઇરિશ ગણિતશાસ્ત્રી, મિકેનિક અને સૈદ્ધાંતિક ભૌતિકશાસ્ત્રી, સર વિલિયમ રોવાન હેમિલ્ટન (1805-1865) દ્વારા તેમના ક્વાટર્નિયન કેલ્ક્યુલસના માળખામાં પ્રકાશિત કરવામાં આવ્યા હતા. વૈજ્ઞાનિકે "વેક્ટર" શબ્દનો પ્રસ્તાવ મૂક્યો અને વેક્ટર પરની કેટલીક કામગીરીનું વર્ણન કર્યું. બ્રિટિશ ભૌતિકશાસ્ત્રી, ગણિતશાસ્ત્રી અને મિકેનિક જેમ્સ ક્લાર્ક મેક્સવેલ (1831-1879) દ્વારા ઇલેક્ટ્રોમેગ્નેટિઝમ પરના કાર્યને આભારી વેક્ટર કેલ્ક્યુલસનો વધુ વિકાસ થયો હતો. 1880 ના દાયકામાં, અમેરિકન ભૌતિકશાસ્ત્રી, ભૌતિક રસાયણશાસ્ત્રી, ગણિતશાસ્ત્રી અને મિકેનિક જોસિયાહ વિલાર્ડ ગિબ્સ (1839-1903) દ્વારા "એલિમેન્ટ્સ ઑફ વેક્ટર એનાલિસિસ" પુસ્તક પ્રકાશિત થયું હતું. આધુનિક વેક્ટર વિશ્લેષણનું વર્ણન 1903 માં અંગ્રેજી સ્વ-શિક્ષિત વૈજ્ઞાનિક, એન્જિનિયર, ગણિતશાસ્ત્રી અને ભૌતિકશાસ્ત્રી ઓલિવર હેવિસાઇડ (1850-1925) દ્વારા કરવામાં આવ્યું હતું.

વ્યાખ્યા

લંબાઈઅથવા વેક્ટર મોડ્યુલનિર્દેશિત સેગમેન્ટની લંબાઈ છે જે વેક્ટરને વ્યાખ્યાયિત કરે છે. તે તરીકે સૂચવવામાં આવે છે.

વેક્ટરના મૂળભૂત પ્રકારો

શૂન્ય વેક્ટરએક વેક્ટર છે જેનો પ્રારંભ બિંદુ અને અંતિમ બિંદુ એકરૂપ છે. શૂન્ય વેક્ટરની લંબાઈ શૂન્ય છે.

એક સીધી રેખાને સમાંતર અથવા એક સીધી રેખા પર આવેલા વેક્ટર કહેવામાં આવે છે સમરેખા(ફિગ. 2).

સહ-નિર્દેશિતજો તેમની દિશાઓ સમાન હોય.

આકૃતિ 2 માં, આ વેક્ટર છે અને. વેક્ટર્સની સહ-દિશા નીચે મુજબ સૂચવવામાં આવે છે:

બે કોલિનિયર વેક્ટર કહેવામાં આવે છે વિરુદ્ધ નિર્દેશિતજો તેમની દિશાઓ વિરુદ્ધ હોય.

આકૃતિ 3 માં, આ વેક્ટર છે અને. હોદ્દો:.