Koha totale e fluturimit në një kënd me horizontin. Studimi i lëvizjes së një trupi të hedhur në një kënd në horizontale

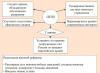
Kjo është një detyrë krijuese për një klasë master në shkencat kompjuterike për nxënësit e shkollave në FEFU.
Qëllimi i detyrës është të zbuloni se si do të ndryshojë trajektorja e trupit nëse merret parasysh rezistenca e ajrit. Është gjithashtu e nevojshme t'i përgjigjemi pyetjes nëse distanca e fluturimit do të arrijë akoma vlerën e saj maksimale në një kënd hedhjeje prej 45 °, nëse merret parasysh rezistenca e ajrit.

Seksioni "Kërkim analitik" përshkruan teorinë. Ky seksion mund të anashkalohet, por duhet të jetë kryesisht i qartë për ju sepse... O pjesën më të madhe të kësaj e keni mësuar në shkollë.
Seksioni "Studimi numerik" përmban një përshkrim të algoritmit që duhet të zbatohet në një kompjuter. Algoritmi është i thjeshtë dhe konciz, kështu që të gjithë duhet të jenë në gjendje ta bëjnë atë.

Hulumtim analitik

Le të prezantojmë një sistem koordinativ drejtkëndor siç tregohet në figurë. Në momentin fillestar të kohës një trup me masë m ndodhet në origjinë. Vektori i nxitimit të rënies së lirë drejtohet vertikalisht poshtë dhe ka koordinata (0, - g).
- vektori i shpejtësisë fillestare. Le ta zgjerojmë këtë vektor në bazën e tij:

. Këtu, ku është madhësia e vektorit të shpejtësisë, është këndi i hedhjes.

Le të shkruajmë ligjin e dytë të Njutonit: .
Nxitimi në çdo moment të kohës është shpejtësia (e menjëhershme) e ndryshimit të shpejtësisë, domethënë derivati i shpejtësisë në lidhje me kohën: .

Prandaj, ligji i 2-të i Njutonit mund të rishkruhet si më poshtë:
, ku është rezultati i të gjitha forcave që veprojnë në trup.
Meqenëse forca e gravitetit dhe forca e rezistencës së ajrit veprojnë në trup, atëherë
.

Ne do të shqyrtojmë tre raste:
1) Forca e rezistencës së ajrit është 0: .
2) Forca e rezistencës së ajrit drejtohet në mënyrë të kundërt me vektorin e shpejtësisë dhe madhësia e saj është proporcionale me shpejtësinë: .
3) Forca e rezistencës së ajrit drejtohet në mënyrë të kundërt me vektorin e shpejtësisë dhe madhësia e saj është proporcionale me katrorin e shpejtësisë: .

Le të shqyrtojmë së pari rastin e parë.
Në këtë rast , ose .

Nga kjo rrjedh se (lëvizje e përshpejtuar në mënyrë të njëtrajtshme).
sepse ( r- vektori i rrezes), pastaj .
Nga këtu .
Kjo formulë nuk është gjë tjetër veçse formula e njohur për ligjin e lëvizjes së një trupi gjatë lëvizjes së përshpejtuar uniformisht.
Që atëherë .
Duke marrë parasysh që të dyja , marrim barazi skalare nga barazia e fundit vektoriale:

Le të analizojmë formulat që rezultojnë.
Le të gjejmë koha e fluturimit Trupat. Duke barazuar y në zero, marrim

Gama e fluturimit e barabartë me vlerën e koordinatave x në një moment në kohë t 0:

Nga kjo formulë del se diapazoni maksimal i fluturimit arrihet në .
Tani le të gjejmë ekuacioni i traktorit të trupit. Për ta bërë këtë, ne shprehemi t përmes x

Dhe le të zëvendësojmë shprehjen që rezulton me t në barazi për y.

Funksioni që rezulton y(x) është një funksion kuadratik, grafiku i tij është një parabolë, degët e së cilës janë të drejtuara poshtë.
Lëvizja e një trupi të hedhur në një kënd me horizontin (pa marrë parasysh rezistencën e ajrit) përshkruhet në këtë video.

Tani merrni parasysh rastin e dytë: .

Ligji i dytë merr formën ,
nga këtu .
Le ta shkruajmë këtë barazi në formë skalare:

Ne kemi dy ekuacione diferenciale lineare.
Ekuacioni i parë ka një zgjidhje

Kjo mund të verifikohet duke zëvendësuar këtë funksion në ekuacionin për v x dhe në gjendjen fillestare .
Këtu e = 2.718281828459... është numri i Euler-it.
Ekuacioni i dytë ka një zgjidhje

Sepse , , atëherë në prani të rezistencës së ajrit lëvizja e trupit priret të jetë uniforme, në ndryshim nga rasti 1, kur shpejtësia rritet pa kufi.
Videoja e mëposhtme thotë se parashutisti së pari lëviz me një ritëm të përshpejtuar, dhe më pas fillon të lëvizë në mënyrë të barabartë (edhe para se të hapet parashuta).

Le të gjejmë shprehje për x Dhe y.
Sepse x(0) = 0, y(0) = 0, atëherë

Na mbetet të shqyrtojmë rastin 3, kur

.
Ligji i dytë i Njutonit ka formën

, ose

.
Në formë skalare, ky ekuacion duket si:

Kjo sistemi jolinear ekuacionet diferenciale . Ky sistem nuk mund të zgjidhet në mënyrë eksplicite, prandaj është e nevojshme të përdoret simulimi numerik.

Studim numerik

Në pjesën e mëparshme pamë se në dy rastet e para ligji i lëvizjes së një trupi mund të merret në formë të qartë. Megjithatë, në rastin e tretë është e nevojshme që problemi të zgjidhet numerikisht. Duke përdorur metoda numerike do të marrim vetëm një zgjidhje të përafërt, por do të jemi mjaft të kënaqur me një saktësi të vogël. (Numri π ose rrënja katrore e 2, nga rruga, nuk mund të shkruhet absolutisht saktësisht, kështu që kur llogariten, ata marrin një numër të kufizuar shifrash, dhe kjo është mjaft e mjaftueshme.)

Ne do të shqyrtojmë rastin e dytë, kur forca e rezistencës së ajrit përcaktohet nga formula . Vini re se kur k= 0 marrim rastin e parë.

Shpejtësia e trupit u bindet ekuacioneve të mëposhtme:

Komponentët e nxitimit janë shkruar në anën e majtë të këtyre ekuacioneve .
Kujtoni se nxitimi është shpejtësia (e menjëhershme) e ndryshimit të shpejtësisë, domethënë derivati i shpejtësisë në lidhje me kohën.
Anët e djathtë të ekuacioneve përmbajnë komponentët e shpejtësisë. Kështu, këto ekuacione tregojnë se si shpejtësia e ndryshimit të shpejtësisë lidhet me shpejtësinë.

Le të përpiqemi të gjejmë zgjidhje për këto ekuacione duke përdorur metoda numerike. Për ta bërë këtë, ne prezantojmë në boshtin kohor rrjetë: le të zgjedhim një numër dhe të shqyrtojmë momentet kohore të formës: .

Detyra jonë është të llogarisim përafërsisht vlerat në nyjet e rrjetit.

Le të zëvendësojmë nxitimin në ekuacionet ( shpejtësia e menjëhershme shpejtësia ndryshon) nga Shpejtësia mesatare ndryshimet në shpejtësi, duke marrë parasysh lëvizjen e një trupi gjatë një periudhe kohore:

Tani le t'i zëvendësojmë përafrimet e marra në ekuacionet tona.

Formulat që rezultojnë na lejojnë të llogarisim vlerat e funksioneve në nyjen tjetër të rrjetit, nëse dihen vlerat e këtyre funksioneve në nyjen e mëparshme të rrjetit.

Duke përdorur metodën e përshkruar, mund të marrim një tabelë të vlerave të përafërta të komponentëve të shpejtësisë.

Si të gjendet ligji i lëvizjes së trupit, d.m.th. tabela e vlerave të përafërta të koordinatave x(t), y(t)? Po kështu!
Ne kemi

Vlera e vx[j] është e barabartë me vlerën e funksionit dhe e njëjtë për vargjet e tjera.
Tani mbetet vetëm të shkruajmë një lak, brenda të cilit do të llogarisim vx duke përdorur vlerën tashmë të llogaritur vx[j], dhe e njëjta gjë me pjesën tjetër të vargjeve. Cikli do të jetë j nga 1 në N.
Mos harroni të inicializoni vlerat fillestare vx, vy, x, y sipas formulave, x 0 = 0, y 0 = 0.

Në Pascal dhe C, ekzistojnë funksionet sin(x) dhe cos(x) për llogaritjen e sinusit dhe kosinusit. Vini re se këto funksione marrin një argument në radianë.

Duhet të ndërtoni një grafik të lëvizjes së trupit gjatë k= 0 dhe k> 0 dhe krahasoni grafikët që rezultojnë. Grafikët mund të krijohen në Excel.
Vini re se formulat e llogaritjes janë aq të thjeshta sa mund të përdorni vetëm Excel për llogaritjet dhe as të përdorni një gjuhë programimi.
Sidoqoftë, në të ardhmen do t'ju duhet të zgjidhni një problem në CATS, në të cilin duhet të llogaritni kohën dhe diapazonin e fluturimit të një trupi, ku nuk mund të bëni pa një gjuhë programimi.

Ju lutemi vini re se mundeni provë programin tuaj dhe kontrolloni grafikët tuaj duke krahasuar rezultatet e llogaritjes kur k= 0 s formulat e sakta dhënë në rubrikën “Kërkim analitik”.

Eksperimentoni me programin tuaj. Sigurohuni që nëse nuk ka rezistencë ajri ( k= 0) diapazoni maksimal i fluturimit me një shpejtësi fillestare fikse arrihet në një kënd prej 45°.
Po në lidhje me rezistencën e ajrit? Në çfarë këndi arrihet diapazoni maksimal i fluturimit?

Figura tregon trajektoret e trupit në v 0 = 10 m/s, α = 45°, g= 9,8 m/s 2, m= 1 kg, k= 0 dhe 1 të marra nga simulimi numerik në Δ t = 0,01.

Ju mund të njiheni me punën e mrekullueshme të nxënësve të klasës së 10-të nga Troitsk, të paraqitur në konferencën "Start in Science" në 2011. Puna i kushtohet modelimit të lëvizjes së një topi tenisi të hedhur në një kënd me horizontin (duke marrë parasysh ajrin rezistencë). Përdoren si modelimi numerik ashtu edhe eksperimenti në shkallë të plotë.

Kështu, kjo detyrë krijuese ju lejon të njiheni me metodat e modelimit matematik dhe numerik, të cilat përdoren në mënyrë aktive në praktikë, por studiohen pak në shkollë. Për shembull, këto metoda u përdorën në zbatimin e projekteve bërthamore dhe hapësinore në BRSS në mesin e shekullit të 20-të.

Nëse një trup hidhet në një kënd me horizontin, atëherë gjatë fluturimit veprohet nga forca e gravitetit dhe forca e rezistencës së ajrit. Nëse forca e rezistencës neglizhohet, atëherë e vetmja forcë që mbetet është graviteti. Prandaj, për shkak të ligjit të 2-të të Njutonit, trupi lëviz me nxitim të barabartë me nxitimin e gravitetit; projeksionet e nxitimit mbi boshtet koordinative ax = 0, ay = - g.

Figura 1. Karakteristikat kinematike të një trupi të hedhur në një kënd me horizontalen

Çdo lëvizje komplekse e një pike materiale mund të përfaqësohet si një mbivendosje e lëvizjeve të pavarura përgjatë boshteve koordinative, dhe në drejtim të akseve të ndryshme lloji i lëvizjes mund të ndryshojë. Në rastin tonë, lëvizja e një trupi fluturues mund të përfaqësohet si mbivendosje e dy lëvizjeve të pavarura: lëvizje uniforme përgjatë boshtit horizontal (boshti X) dhe lëvizje e përshpejtuar në mënyrë të njëtrajtshme përgjatë boshtit vertikal (boshti Y) (Fig. 1). .

Prandaj, parashikimet e shpejtësisë së trupit ndryshojnë me kalimin e kohës si më poshtë:

ku $v_0$ është shpejtësia fillestare, $(\mathbf \alpha )$ është këndi i hedhjes.

Me zgjedhjen tonë të origjinës, koordinatat fillestare (Fig. 1) janë $x_0=y_0=0$. Pastaj marrim:

(1)

Le të analizojmë formulat (1). Le të përcaktojmë kohën e lëvizjes së trupit të hedhur. Për ta bërë këtë, le të vendosim koordinatën y të barabartë me zero, sepse në momentin e uljes lartësia e trupit është zero. Nga këtu marrim për kohën e fluturimit:

Vlera e dytë kohore në të cilën lartësia është zero është zero, që i përgjigjet momentit të hedhjes, d.m.th. kjo vlerë ka edhe një kuptim fizik.

Gama e fluturimit e marrim nga formula e parë (1). Gama e fluturimit është vlera e koordinatës x në fund të fluturimit, d.m.th. në një kohë të barabartë me $t_0$. Duke zëvendësuar vlerën (2) në formulën e parë (1), marrim:

Nga kjo formulë mund të shihet se diapazoni më i madh i fluturimit arrihet në një kënd hedhjeje prej 45 gradë.

Lartësia maksimale e ngritjes së trupit të hedhur mund të merret nga formula e dytë (1). Për ta bërë këtë, ju duhet të zëvendësoni një vlerë kohore të barabartë me gjysmën e kohës së fluturimit (2) në këtë formulë, sepse Është në mes të trajektores që lartësia e fluturimit është maksimale. Duke kryer llogaritjet, marrim

Nga ekuacionet (1) mund të merret ekuacioni i trajektores së trupit, d.m.th. një ekuacion që lidh koordinatat x dhe y të një trupi gjatë lëvizjes. Për ta bërë këtë, duhet të shprehni kohën nga ekuacioni i parë (1):

dhe zëvendësojeni atë në ekuacionin e dytë. Pastaj marrim:

Ky ekuacion është ekuacioni i trajektores së lëvizjes. Mund të shihet se ky është ekuacioni i një parabole me degët e saj poshtë, siç tregohet nga shenja "-" përpara termit kuadratik. Duhet pasur parasysh se këndi i hedhjes $\alpha $ dhe funksionet e tij janë thjesht konstante këtu, d.m.th. numra konstante.

Një trup hidhet me shpejtësi v0 në një kënd $(\mathbf \alpha )$ në horizontale. Koha e fluturimit $t = 2 s$. Deri në çfarë lartësie Hmax do të ngrihet trupi?

$$t_B = 2 s$$ $$H_max - ?$$

Ligji i lëvizjes së trupit ka formën:

$$\left\( \fillimi(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \djathtas.$ $

Vektori i shpejtësisë fillestare formon një kënd $(\mathbf \alpha )$ me boshtin OX. Prandaj,

\ \ \

Një gur hidhet nga maja e një mali në një kënd = 30$()^\circ$ në horizont me një shpejtësi fillestare prej $v_0 = 6 m/s$. Këndi i planit të pjerrët = 30$()^\circ$. Në çfarë largësie nga pika e hedhjes do të bjerë guri?

$$ \alfa =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Le të vendosim origjinën e koordinatave në pikën e hedhjes, OX - përgjatë rrafshit të pjerrët poshtë, OY - pingul me rrafshin e prirur lart. Karakteristikat kinematike të lëvizjes:

Ligji i lëvizjes:

$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2 \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \djathtas.$$ \

Duke zëvendësuar vlerën që rezulton $t_В$, gjejmë $S$:

Gama maksimale e një guri të shkrepur nga një katapultë e palëvizshme është S = 22,5 m. Gjeni gamën maksimale të mundshme të një guri të shkrepur nga i njëjti katapultë i montuar në një platformë që lëviz horizontalisht me një shpejtësi konstante v = 15,0 m/s. Injoroni rezistencën e ajrit, llogaritni nxitimin e rënies së lirë g = 10,0 m/s 2.

Zgjidhja: Dihet mirë se diapazoni maksimal i fluturimit të një trupi të hedhur në një kënd me horizontalen arrihet në një kënd nisjeje të barabartë me 45° dhe përcaktohet nga formula:

Le të shqyrtojmë tani fluturimin e një guri të lëshuar nga një katapultë lëvizëse. Le të prezantojmë një sistem koordinativ, boshtet e të cilit janë: X- drejtuar horizontalisht, dhe Y- vertikalisht. Origjina e koordinatave është në përputhje me pozicionin e katapultës në momentin e lëshimit të gurit.

Për të llogaritur vektorin e shpejtësisë së gurit, është e nevojshme të merret parasysh shpejtësia horizontale e katapultës v = v o. Le të themi se një katapultë hedh një gur në një kënd α në horizont. Atëherë përbërësit e shpejtësisë fillestare të gurit në sistemin tonë koordinativ mund të shkruhen si:

Duke e zëvendësuar këtë shprehje në ekuacionin e parë të sistemit (3), marrim diapazonin e fluturimit të gurit:

Së dyti, nuk rrjedh fare nga (5) se S 1 do të jetë maksimale në α = 45°(kjo është e vërtetë për (6), kur v=0).

Duke propozuar këtë problem për Olimpiadën Republikane, autorët ishin të bindur se nëntë të dhjetat e pjesëmarrësve do të merrnin formulën (5) dhe më pas do ta zëvendësonin vlerën në të. α = 45°. Sidoqoftë, për keqardhjen tonë, gabuam: asnjë olimpist i vetëm nuk dyshoi se diapazoni maksimal i fluturimit arrihet gjithmonë (!) në një kënd nisjeje të barabartë me 45°. Ky fakt i njohur ka zbatueshmëri të kufizuar: është e vërtetë vetëm nëse:

a) mos merrni parasysh rezistencën e ajrit;
b) pika e ngritjes dhe pika e rënies janë në të njëjtin nivel;
c) predha është e palëvizshme.

Le të kthehemi te zgjidhja e problemit. Pra, ne duhet të gjejmë vlerën e këndit α , në të cilën S 1 e përcaktuar me formulën (5), është maksimumi. Sigurisht, mund të gjeni ekstremin e funksionit duke përdorur aparatin e llogaritjes diferenciale: gjeni derivatin, vendoseni atë të barabartë me zero dhe, pasi të keni zgjidhur ekuacionin që rezulton, gjeni vlerën e dëshiruar. α . Mirëpo, duke qenë se problemi u është propozuar nxënësve të klasës së 9-të, do të japim zgjidhjen gjeometrike të saj. Le të përfitojmë nga fakti se v = v o = 15 m/s.

Le t'i renditim vektorët v Dhe v o siç tregohet në fig. Meqenëse gjatësitë e tyre janë të barabarta, rreth tyre mund të përshkruhet një rreth me qendër në pikën O. Pastaj gjatësia e segmentit A.C. e barabartë me v o + v o cos α(kjo është vxo), dhe gjatësinë e segmentit B.C. e barabartë me v o mëkat α(Kjo vyo). Produkti i tyre është i barabartë me dyfishin e sipërfaqes së trekëndëshit ABC, ose zona e trekëndëshit ABB 1.

Ju lutemi vini re se është produkti që përfshihet në shprehjen për diapazonin e fluturimit (5). Me fjalë të tjera, diapazoni i fluturimit është i barabartë me produktin e zonës DAVV 1 nga një faktor konstant 2/g.

Tani le të pyesim veten: cili nga trekëndëshat e gdhendur në një rreth të caktuar ka sipërfaqen maksimale? Natyrisht e saktë! Prandaj, vlera e dëshiruar e këndit α = 60°.

Vektor AB ekziston një vektor i shpejtësisë totale fillestare të gurit, ai drejtohet në një kënd 30° në horizont (përsëri, aspak 45°).

Kështu, zgjidhja përfundimtare e problemit rrjedh nga formula (5), në të cilën duhet të zëvendësojmë α = 60°.

Teoria

Çdo lëvizje komplekse pika materiale mund të paraqitet si një mbivendosje e lëvizjeve të pavarura përgjatë boshteve koordinative, dhe në drejtim të akseve të ndryshme lloji i lëvizjes mund të ndryshojë. Në rastin tonë, lëvizja e një trupi fluturues mund të përfaqësohet si mbivendosje e dy lëvizjeve të pavarura: lëvizje uniforme përgjatë boshtit horizontal (boshti X) dhe lëvizje e përshpejtuar në mënyrë të njëtrajtshme përgjatë boshtit vertikal (boshti Y) (Fig. 1). .

Prandaj, parashikimet e shpejtësisë së trupit ndryshojnë me kalimin e kohës si më poshtë:

ku është shpejtësia fillestare, α është këndi i hedhjes.

Prandaj, koordinatat e trupit ndryshojnë si kjo:

Me zgjedhjen tonë të origjinës së koordinatave, koordinatat fillestare (Fig. 1) Pastaj

Vlera e dytë kohore në të cilën lartësia është zero është zero, që i përgjigjet momentit të hedhjes, d.m.th. kjo vlerë ka edhe një kuptim fizik.

Gama e fluturimit e marrim nga formula e parë (1). Gama e fluturimit është vlera e koordinatave X në fund të fluturimit, d.m.th. në një kohë të barabartë me t 0. Duke zëvendësuar vlerën (2) në formulën e parë (1), marrim:

(3)

Nga kjo formulë mund të shihet se diapazoni më i madh i fluturimit arrihet në një kënd hedhjeje prej 45 gradë.

Udhëzimet

Le të hidhet një trup në një kënd α në horizont me një shpejtësi fillestare v0. Le të jenë zero koordinatat fillestare të trupit: x(0)=0, y(0)=0. Në projeksionet në boshtet e koordinatave, shpejtësia fillestare do të zbërthehet në dy komponentë: v0(x) dhe v0(y). E njëjta shpejtësi në përgjithësi. Përgjatë boshtit Ox, shpejtësia konvencionalisht konsiderohet konstante, ndërsa përgjatë boshtit Oy ndryshon nën ndikimin e . Përshpejtimi i gravitetit g mund të merret përafërsisht 10 m/s².

Këndi α në të cilin hidhet trupi nuk jepet rastësisht. Nëpërmjet tij mund të përshkruani shpejtësinë fillestare në akset koordinative. Kështu, v0(x)=v0·cos(α), v0(y)=v0·sin(α). Tani mund të marrim funksionin e komponentëve të koordinatave të shpejtësisë: v(x)=const=v0(x)=v0·cos(α), v(y)=v0(y)-g·t=v0·sin( α)-g· t.

Koordinatat x dhe y të trupit varen nga koha t. Kështu, ne mund të krijojmë dy ekuacione varësie: x=x0+v0(x) t+a(x) t²/2, y=y0+v0(y) t+a(y) t²/2. Meqenëse x0=0, a(x)=0, atëherë x=v0(x) t=v0 cos(α) t. Dihet gjithashtu se y0=0, a(y)=-g (shenja “ ” shfaqet sepse drejtimi i nxitimit të gravitetit g dhe drejtimi pozitiv i boshtit Oy janë të kundërta). Prandaj y=v0·sin(α)·t-g·t²/2.

Koha e fluturimit mund të shprehet nga formula e shpejtësisë, duke ditur që në pikën maksimale trupi ndalon për një çast (v = 0), dhe kohëzgjatja e "ngritjes" dhe "zbritjes" është e barabartë. Pra, kur zëvendësohet v(y)=0 në ekuacionin v(y)=v0·sin(α)-g·t rezulton: 0=v0·sin(α)-g·t(p), ku t. (p) – koha e pikut, “t kulm”. Prandaj t(p)=v0·sin(α)/g. Koha totale e fluturimit do të shprehet më pas si t=2·v0·sin(α)/g.

E njëjta formulë mund të merret në një mënyrë tjetër, matematikisht, nga ekuacioni i koordinatës y=v0·sin(α)·t-g·t²/2. Ky ekuacion mund të rishkruhet në një formë paksa të modifikuar: y=-g/2·t²+v0·sin(α)·t. Mund të shihet se kjo është një varësi kuadratike, ku y është një funksion, t është një argument. Kulmi i parabolës që përshkruan trajektoren është pika t(p)=[-v0·sin(α)]/[-2g/2]. Minuset dhe dyshe anulohen, pra t(p)=v0·sin(α)/g. Nëse lartësinë maksimale e shënojmë si H dhe kujtojmë se pika e pikut është kulmi i parabolës përgjatë së cilës lëviz trupi, atëherë H=y(t(p))=v0²sin²(α)/2g. Kjo do të thotë, për të marrë lartësinë, duhet të zëvendësoni "kulmin t" në ekuacionin për koordinatën y.

Pra, koha e fluturimit shkruhet si t=2·v0·sin(α)/g. Për ta ndryshuar atë, duhet të ndryshoni shpejtësinë fillestare dhe këndin e prirjes në përputhje me rrethanat. Sa më e lartë të jetë shpejtësia, aq më gjatë fluturon trupi. Me një kënd është disi më e ndërlikuar, sepse koha nuk varet nga vetë këndi, por nga sinusi i tij. Maksimumi kuptimi i mundshëm sinus – unitet – arrihet në një kënd të pjerrësisë 90°. Kjo do të thotë që një trup fluturon më gjatë kur hidhet vertikalisht lart.

Gama e fluturimit është koordinata përfundimtare x. Nëse e zëvendësojmë kohën e gjetur tashmë të fluturimit në ekuacionin x=v0·cos(α)·t, atëherë është e lehtë të gjejmë se L=2v0²sin(α)cos(α)/g. Këtu mund të aplikoni formula trigonometrike kënd i dyfishtë 2sin(α)cos(α)=sin(2α), pastaj L=v0²sin(2α)/g. Sinusi i dy alfave është i barabartë me një kur 2α=n/2, α=n/4. Kështu, diapazoni i fluturimit është maksimal nëse trupi hidhet në një kënd prej 45°.