Vektoriai: apibrėžimas ir pagrindinės sąvokos. Vektoriai kompiuteriniuose žaidimuose Vektoriai guli

Detaliau šios formulės nekalbėsime. Be to, tai gana sunku įsiminti. Prie šio taško grįšime susipažinę su lemiančiais veiksniais.

Na, o bendram vystymuisi naudinga žinoti, kad gauto vektoriaus ilgis yra lygus lygiagretainio, pastatyto ant vektorių, plotui a ir b.

Vektorių normalizavimas

Normalizuotas vektorius yra vektorius, kurio ilgis yra vienas.

Normalizuoto vektoriaus radimo formulė yra tokia - visi vektoriaus komponentai turi būti padalyti iš jo ilgio:

v n = v/ | v | =

Pokalbis

Kaip tikriausiai matėte, vektorius suprasti nėra sunku. Mes apžvelgėme keletą operacijų su vektoriais.

Kituose „matematikos“ skyriaus straipsniuose aptarsime matricas, determinantus, tiesinių lygčių sistemas. Visa tai yra teorija.

Po to pažvelgsime į matricų transformacijas. Tada suprasite, kokia svarbi matematika kuriant kompiuterinius žaidimus. Ši tema tiesiog taps visų ankstesnių temų praktika.

Apibrėžimas Iškviečiama sutvarkyta rinkinys (x 1, x 2, ..., x n) n realiųjų skaičių n matmenų vektorius, o skaičiai x i (i = 1, ..., n) yra komponentai, arba koordinates,

Pavyzdys. Jei, pavyzdžiui, tam tikroje automobilių gamykloje per pamainą reikia pagaminti 50 lengvųjų automobilių, 100 sunkvežimių, 10 autobusų, 50 komplektų atsarginių dalių lengviesiems automobiliams ir 150 komplektų sunkvežimiams ir autobusams, tai šios gamyklos gamybos programą galima įrašyti vektoriaus forma (50, 100 , 10, 50, 150), kuri turi penkis komponentus.

Žymėjimas. Vektoriai žymimi paryškintomis mažosiomis raidėmis arba raidėmis su juostele arba rodykle viršuje, pavyzdžiui, a arba . Du vektoriai vadinami lygus jeigu jie turi vienodą skaičių komponentų ir atitinkami jų komponentai yra vienodi.

Vektoriaus komponentai negali būti sukeisti, pavyzdžiui, (3, 2, 5, 0, 1) ir (2, 3, 5, 0, 1) yra skirtingi vektoriai.
Veiksmai su vektoriais. Pagal gaminįx= (x 1, x 2, ..., x n) realiuoju skaičiumi λ vadinamas vektoriumi λ x= (λ x 1, λ x 2, ..., λ x n).

Sumax= (x 1, x 2, ..., x n) ir y= (y 1, y 2, ..., y n) vadinamas vektoriumi x + y= (x 1 + y 1, x 2 + y 2, ..., x n + + y n).

Vektorių erdvė. N-matmenų vektorinė erdvė R n apibrėžiamas kaip visų n matmenų vektorių aibė, kuriai apibrėžtos daugybos iš realiųjų skaičių ir sudėjimo operacijos.

Ekonominė iliustracija. Ekonominė n-matės vektorinės erdvės iliustracija: prekių erdvė (prekės). Pagal prekė suprasime kokią nors prekę ar paslaugą, kuri tam tikru laiku buvo parduota tam tikroje vietoje. Tarkime, kad po ranka yra baigtinis daiktų skaičius, n; kiekvienos iš jų vartotojo įsigytus kiekius apibūdina prekių rinkinys

x= (x 1, x 2, ..., x n),

čia x i žymi vartotojo įsigytos i-osios prekės kiekį. Darysime prielaidą, kad visos prekės turi savavališko dalijimosi savybę, kad būtų galima nusipirkti bet kokį neneigiamą kiekvienos iš jų kiekį. Tada visos galimos prekių aibės yra prekių erdvės vektoriai C = ( x= (x 1, x 2, ..., x n) x i ≥ 0, i = 1, ..., n).

Linijinė nepriklausomybė. Sistema e 1 , e 2 , ... , e m n matmenų vektoriai vadinami tiesiškai priklausomas jei yra tokių skaičių λ 1, λ 2, ..., λ m, kad bent vienas iš jų būtų lygus nuliui, kad λ 1 e 1 + λ m e m = 0; kitaip ši vektorių sistema vadinama tiesiškai nepriklausomas, tai yra, nurodyta lygybė galima tik tuo atveju, kai visi λ 1 = λ 2 = ... = λ m = 0. Vektorių tiesinės priklausomybės geometrinė reikšmė R 3, interpretuojami kaip nukreipti segmentai, paaiškinkite šias teoremas.

1 teorema. Sistema, susidedanti iš vieno vektoriaus, yra tiesiškai priklausoma tada ir tik tada, kai šis vektorius yra lygus nuliui.

2 teorema. Tam, kad du vektoriai būtų tiesiškai priklausomi, būtina ir pakanka, kad jie būtų kolineariniai (lygiagrečiai).

3 teorema ... Tam, kad trys vektoriai būtų tiesiškai priklausomi, būtina ir pakanka, kad jie būtų vienodi (gulėtų toje pačioje plokštumoje).

Kairysis ir dešinysis vektorių tripletai. Trys nevienaplaniai vektoriai a, b, c paskambino teisingai jei stebėtojas iš jų bendros kilmės kerta vektorių galus a, b, c rodoma tvarka, atrodo, kad jis yra pagal laikrodžio rodyklę. Priešingu atveju a, b, c -kairysis trigubas... Vadinami visi dešinieji (arba kairieji) vektorių tripletai vienodai orientuotas.

Pagrindas ir koordinatės. Troika e 1, e 2 , e 3 nevienaplaniai vektoriai in R 3 vadinamas pagrindu, ir patys vektoriai e 1, e 2 , e 3 - pagrindinis... Bet koks vektorius a galima vienareikšmiškai išplėsti bazinių vektorių atžvilgiu, tai yra, pavaizduoti formoje

a= x 1 e 1 + x 2 e 2 + x 3 e 3, (1.1)

vadinami skaičiai x 1, x 2, x 3 plėtinyje (1.1). koordinatesa pagrinde e 1, e 2 , e 3 ir pažymėtas a(x 1, x 2, x 3).

Ortonormalus pagrindas. Jei vektoriai e 1, e 2 , e 3 yra poromis statmenos ir kiekvieno iš jų ilgis lygus vienetui, tada vadinamas pagrindas ortonormalus, ir koordinatės x 1, x 2, x 3 - stačiakampio formos. Ortonormaliojo pagrindo baziniai vektoriai bus pažymėti i, j, k.

Mes manysime, kad erdvėje R 3, pasirinkta teisinga Dekarto stačiakampių koordinačių sistema (0, i, j, k}.

Vektorinis produktas.Vektorinis produktasa vienam vektoriui b vadinamas vektoriumi c, kuris nustatomas pagal šias tris sąlygas:

1. Vektoriaus ilgis c yra skaitine prasme lygi lygiagretainio, sudaryto ant vektorių, plotui a ir b, t.y.
c= | a || b | nuodėmė ( a^b).

2. Vektorius c statmenai kiekvienam vektoriui a ir b.

3. Vektoriai a, b ir c paimtas nurodyta tvarka suformuoja dešinįjį trigubą.

Dėl vektorinio produkto cįvedamas žymėjimas c =[ab] arba
c = a × b.

Jei vektoriai a ir b kolinearinis, tada nuodėmė ( a ^ b) = 0 ir [ ab] = 0, ypač [ aa] = 0. Vienetinių vektorių vektorinės sandaugos: [ ij]=k, [jk] = i, [ki]=j.

Jei vektoriai a ir b pateikta pagrinde i, j, k koordinates a(1, 2, 3), b(b 1, b 2, b 3), tada

Mišrus darbas. Jei dviejų vektorių kryžminė sandauga a ir b skaliaras, padaugintas iš trečiojo vektoriaus c, tada vadinama tokia trijų vektorių sandauga mišrus darbas ir žymimas simboliu a b c.

Jei vektoriai a, b ir c pagrinde i, j, k pateiktos pagal jų koordinates
a(1, 2, 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), tada

.

Mišrus sandauga turi paprastą geometrinę interpretaciją – tai skaliaras, absoliučia verte lygus gretasienio, pastatyto ant šių trijų vektorių, tūriui.

Jei vektoriai sudaro dešinįjį tripletą, tada jų mišrus sandauga yra teigiamas skaičius, lygus nurodytam tūriui; jei trys a, b, c - tada paliko a b c<0 и V = - a b c, todėl V = | a b c |.

Laikoma, kad vektorių koordinatės, su kuriomis susiduriama pirmojo skyriaus uždaviniuose, pateiktos teisingo ortonormalaus pagrindo atžvilgiu. Vieneto vektorius kartu su vektoriumi a,žymimas simboliu a O. Simbolis r=OM taško M spindulio vektorius žymimas simboliais a, AB arba | a |, |AB | vektorių moduliai a ir AB.

Pavyzdys 1.2. Raskite kampą tarp vektorių a= 2m+4n ir b= m-n, kur m ir n - vienetų vektoriai ir kampas tarp m ir n yra lygus 120 p.

Sprendimas... Turime: cos φ = ab/ab, ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4 + 2cos120 o = - 2 + 2 (-0,5) = -3; a = ; a 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4 + 16 (-0,5) + 16 = 12, taigi a =. b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 = 1-2 (-0,5) +1 = 3, taigi b =. Galiausiai turime: cos φ == -1/2, φ = 120 o.

1.3 pavyzdys.Žinant vektorius AB(-3, -2,6) ir pr. Kr(-2,4,4), apskaičiuokite trikampio ABC aukščio AD ilgį.

Sprendimas... Nurodydami trikampio ABC plotą per S, gauname:
S = 1/2 pr. Kr. Tada AD = 2S / BC, BC = = = 6,
S = 1/2 | AB ×AC |. AC = AB + BC, taigi vektorius AC turi koordinates
.

VEKTORIAUS
Fizikoje ir matematikoje vektorius yra dydis, apibūdinamas jo skaitine verte ir kryptimi. Fizikoje yra daug svarbių dydžių, kurie yra vektoriai, pavyzdžiui, jėga, padėtis, greitis, pagreitis, sukimo momentas, impulsas, elektrinių ir magnetinių laukų stiprumas. Juos galima palyginti su kitais dydžiais, tokiais kaip masė, tūris, slėgis, temperatūra ir tankis, kuriuos galima apibūdinti įprastu skaičiumi, ir jie vadinami „skaliarais“. Vektorinis žymėjimas naudojamas dirbant su reikšmėmis, kurių negalima visiškai nurodyti naudojant įprastus skaičius. Pavyzdžiui, norime apibūdinti objekto padėtį tam tikro taško atžvilgiu. Galime pasakyti, kiek kilometrų nuo taško iki objekto, bet negalime iki galo nustatyti jo vietos, kol nežinome krypties, kuria jis yra. Taigi objekto vieta apibūdinama skaitine verte (atstumas kilometrais) ir kryptimi. Grafiškai vektoriai vaizduojami kaip tam tikro ilgio nukreiptos tiesios linijos atkarpos, kaip parodyta Fig. 1. Pavyzdžiui, norint grafiškai pavaizduoti penkių kilogramų jėgą, jėgos kryptimi reikia nubrėžti penkių vienetų ilgio tiesią atkarpą. Rodyklė rodo, kad jėga veikia nuo A iki B; jei jėga veiktų nuo B iki A, tai rašytume arba Patogumo dėlei vektoriai dažniausiai žymimi paryškintomis didžiosiomis raidėmis (A, B, C ir pan.); vektoriai A ir -A turi vienodas skaitines reikšmes, bet priešinga kryptimi. Skaitinė vektoriaus A reikšmė vadinama moduliu arba ilgiu ir žymima A arba | A |. Šis dydis, žinoma, yra skaliarinis. Vektorius, kurio pradžia ir pabaiga sutampa, vadinamas nuliu ir žymimas O.

Du vektoriai vadinami lygiais (arba laisvaisiais), jei jų moduliai ir kryptys sutampa. Tačiau mechanikoje ir fizikoje šis apibrėžimas turi būti naudojamas atsargiai, nes dvi vienodos jėgos, veikiančios skirtingus kūno taškus, paprastai lems skirtingus rezultatus. Šiuo atžvilgiu vektoriai skirstomi į „susietus“ arba „slenkančius“ taip: Susieti vektoriai turi fiksuotus taikymo taškus. Pavyzdžiui, spindulio vektorius nurodo taško padėtį tam tikros fiksuotos pradžios atžvilgiu. Susiję vektoriai laikomi lygiaverčiais, jei jie turi ne tik tuos pačius modulius ir kryptis, bet ir bendrą taikymo tašką. Slenkantys vektoriai yra lygūs vektoriai, esantys vienoje tiesėje.
Vektorių pridėjimas. Idėja pridėti vektorius kilo dėl to, kad galime rasti vieną vektorių, turintį tokį patį poveikį kaip ir kiti du vektoriai kartu. Jei, norėdami patekti į tam tikrą tašką, pirmiausia turime eiti A kilometrus viena kryptimi, o po to B kilometrus kita kryptimi, tai galutinį tašką galėtume pasiekti eidami C kilometrus trečia kryptimi (2 pav.). . Šia prasme galime pasakyti

Galime pridėti bet kokį vektorių skaičių, o terminų tvarka rezultatui įtakos neturi. Tiesa ir atvirkščiai: bet kuris vektorius suskaidomas į du ar daugiau „komponentų“; į du ar daugiau vektorių, kuriuos pridėjus bus gautas pradinis vektorius. Pavyzdžiui, pav. 2, A ir B yra komponentai C. Daugelis matematinių operacijų su vektoriais supaprastėja, jei vektorius išskaidomas į tris komponentus trimis viena kitai statmenomis kryptimis. Pasirinkime dešiniąją Dekarto koordinačių sistemą su ašimis Ox, Oy ir Oz, kaip parodyta Fig. 5. Dešiniųjų koordinačių sistema reiškia, kad x, y ir z ašys yra išdėstytos taip, kaip atitinkamai gali būti dešinės rankos nykščio, rodomojo ir viduriniojo pirštai. Iš vienos dešiniarankės koordinačių sistemos visada galite gauti kitą dešiniarankių koordinačių sistemą atitinkamai ją pasukdami. Fig. 5, parodytas vektoriaus A išskaidymas į tris komponentus, ir jie susumuojami iki vektoriaus A, nes

Vadinasi,

Taip pat būtų galima pirmiausia pridėti ir gauti, o tada pridėti prie vektoriaus A projekcijų trijose koordinačių ašyse, pažymėtos Ax, Ay ir Az, vadinamos vektoriaus A „skaliariniais komponentais“:

kur a, b ir g yra kampai tarp A ir trijų koordinačių ašių. Dabar pristatome tris i, j ir k vieneto ilgio vektorius (vieneto vektorius), kurių kryptis yra tokia pati kaip ir atitinkamos ašys x, y ir z. Tada, jei Ax padauginamas iš i, gauta sandauga yra vektorius, lygus ir

Du vektoriai yra lygūs tada ir tik tada, kai atitinkami jų skaliariniai komponentai yra vienodi. Taigi A = B tada ir tik tada, kai Ax = Bx, Ay = By, Az = Bz. Sudedant jų komponentus galima pridėti du vektorius:

Be to, pagal Pitagoro teoremą:

Linijinės funkcijos. Išraiška aA + bB, kur a ir b yra skaliarai, vadinama vektorių A ir B tiesine funkcija. Tai vektorius, esantis toje pačioje plokštumoje kaip A ir B; jei A ir B nėra lygiagretūs, tai pasikeitus a ir b vektorius aA + bB judės per visą plokštumą (6 pav.). Jei A, B ir C ne visi yra toje pačioje plokštumoje, tai vektorius aA + bB + cC (a, b ir c pokytis) juda visoje erdvėje. Tarkime, kad A, B ir C yra vienetiniai vektoriai i, j ir k. Vektorius ai yra ant x ašies; vektorius ai + bj gali judėti išilgai visos xy plokštumos; vektorius ai + bj + ck gali judėti visoje erdvėje.

Ir vienas gali tęstis iki penkių, šešių ar bet kokio skaičiaus matmenų. Nors vizualizuoti tokio vektoriaus neįmanoma, matematinių sunkumų čia nekyla. Toks įrašas dažnai praverčia; pavyzdžiui, judančios dalelės būsena apibūdinama šešiamačiu vektoriumi P (x, y, z, px, py, pz), kurio komponentai yra jos padėtis erdvėje (x, y, z) ir impulsas. (px, py, pz). Ši erdvė vadinama „fazės erdve“; jei nagrinėsime dvi daleles, tai fazių erdvė yra 12 matmenų, jei trys, tai 18 ir pan. Matmenų skaičius gali būti didinamas neribotą laiką; tačiau dydžiai, su kuriais kalbėsime, elgiasi taip pat, kaip ir tie, kuriuos nagrinėsime likusioje šio straipsnio dalyje, ty trimačiai vektoriai.
Dviejų vektorių daugyba. Vektorių sudėjimo taisyklė gauta tiriant vektoriais vaizduojamų dydžių elgesį. Nėra jokios akivaizdžios priežasties, kodėl dviejų vektorių jokiu būdu negalima padauginti, tačiau šis dauginimas bus prasmingas tik tuomet, jei parodysite jo matematinį nuoseklumą; be to, pageidautina, kad darbas turėtų tam tikrą fizinę reikšmę. Yra du būdai padauginti vektorius, kurie atitinka šias sąlygas. Vieno iš jų rezultatas yra skaliarinis, tokia sandauga vadinama dviejų vektorių „taškiniu sandauga“ arba „vidiniu sandauga“ ir rašoma ABB arba (A, B). Kitas daugybos rezultatas yra vektorius, vadinamas "vektoriaus sandauga" arba "išoriniu sandauga" ir parašytas A * B arba []. Taškiniai produktai turi fizinę vieno, dviejų arba trijų dimensijų reikšmę, o vektoriniai produktai yra apibrėžti tik trims dimensijoms.
Skaliariniai produktai. Jei, veikiant kokiai nors jėgai F, taškas, į kurį ji veikia, pasislenka atstumu r, tai atliktas darbas yra lygus r ir komponento F sandaugai kryptimi r. Šis komponentas lygus F cos bF, rc, kur bF, rc – kampas tarp F ir r, t.y. Atliktas darbas = Fr cos bF, rc. Tai yra fizinio taško sandaugos, apibrėžtos bet kuriems dviem vektoriams A, B pagal formulę, pagrindimo pavyzdys
A * B = AB cos bA, Bc.
Kadangi visi dydžiai dešinėje lygties pusėje yra skaliarai, tai A * B = B * A; todėl skaliarinė daugyba yra komutacinė. Skaliarinis dauginimas taip pat turi pasiskirstymo savybę: A * (B + C) = A * B + A * C. Jei vektoriai A ir B yra statmeni, tai cos bA, Bc yra lygus nuliui, taigi, A * B = 0, net jei nei A, nei B nėra lygūs nuliui. Štai kodėl negalime dalyti iš vektorių. Tarkime, kad abi lygties A * B = A * C puses padalintume iš A. Tai gautų B = C, o jei būtų galima atlikti padalijimą, tada ši lygybė būtų vienintelis galimas rezultatas. Tačiau jei perrašysime lygtį A * B = A * C į A * (B - C) = 0 ir prisiminsime, kad (B - C) yra vektorius, tada aišku, kad (B - C) nebūtinai yra nulis ir todėl B nebūtinai turi būti lygus C. Šie prieštaringi rezultatai rodo, kad vektorių dalyba yra neįmanoma. Taškinė sandauga suteikia dar vieną būdą užrašyti skaitinę vektoriaus reikšmę (modulį): A * A = AA * cos 0 ° = A2;
todėl

Taškinį sandaugą galima parašyti ir kitaip. Norėdami tai padaryti, atminkite, kad: A = Ax i + Ayj + Azk. pastebėti, kad

Tada

Kadangi paskutinėje lygtyje yra x, y ir z kaip apatiniai indeksai, lygtis, atrodo, priklauso nuo konkrečios pasirinktos koordinačių sistemos. Tačiau taip nėra, kaip matyti iš apibrėžimo, kuris nepriklauso nuo pasirinktų koordinačių ašių.
Vektoriniai meno kūriniai. Vektorius arba išorinė vektorių sandauga yra vektorius, kurio modulis lygus jų modulių sandaugai kampo, statmeno pirminiams vektoriams ir kartu su jais sudarančio dešinįjį trigubą, sinuso. Šį produktą lengviausia pristatyti atsižvelgiant į greičio ir kampinio greičio ryšį. Pirmasis yra vektorius; dabar parodysime, kad pastarasis gali būti interpretuojamas ir kaip vektorius. Besisukančio kūno kampinis greitis nustatomas taip: pasirinkite bet kurį kūno tašką ir iš šio taško nubrėžkite statmeną sukimosi ašiai. Tada kūno kampinis greitis yra radianų skaičius, kuriuo ši linija pasisuko per laiko vienetą. Jei kampinis greitis yra vektorius, jis turi turėti skaitinę reikšmę ir kryptį. Skaitinė reikšmė išreiškiama radianais per sekundę, kryptį galima pasirinkti išilgai sukimosi ašies, ją galima nustatyti nukreipus vektorių ta kryptimi, kuria judėtų dešiniarankis sraigtas besisukantis su kūnu. Apsvarstykite kūno sukimąsi aplink fiksuotą ašį. Jei įtaisysime šią ašį žiedo viduje, kuri savo ruožtu yra pritvirtinta prie ašies, įterptos į kito žiedo vidų, galime pasukti korpusą pirmojo žiedo viduje kampiniu greičiu w1 ir tada priversti vidinį žiedą (ir korpusą) suktis kampinis greitis w2. 7 paveikslas iliustruoja esmę; apskritos rodyklės rodo sukimosi kryptis. Šis kūnas yra kieta sfera, kurios centras O ir spindulys r.

Ryžiai. 7. RUMULĖ, SUKOTA CENTRE O, sukasi kampiniu greičiu w1 žiedo BC viduje, kuris, savo ruožtu, sukasi žiedo DE viduje kampiniu greičiu w2. Sfera sukasi kampiniu greičiu, lygiu kampinių greičių sumai, o visi tiesės POP taškai yra momentinio ramybės būsenoje.

Šis atstumas lygus nuliui, jei

Šiuo atveju taškas P yra momentinio ramybės būsenoje, lygiai taip pat visi tiesės POP taškai. "Likusi sferos dalis judės (apskritimai, kuriais juda kiti taškai, nesiliečia, o susikerta ). Taigi POPў yra momentinė sferos sukimosi ašis, kaip ir ratas, riedantis keliu kiekvienu laiko momentu, sukasi apie žemiausią savo tašką. Koks yra sferos kampinis greitis? Paprastumo dėlei pasirenkame tašką A kurioje ašis w1 kerta paviršių. Šiuo metu, kurį svarstome , ji juda laiku Dt atstumu

Aplink apskritimą, kurio spindulys yra r sin w1. Pagal apibrėžimą kampinis greitis

Iš šios formulės ir santykio (1) gauname

Kitaip tariant, jei užsirašote skaitinę reikšmę ir pasirenkate kampinio greičio kryptį, kaip aprašyta aukščiau, tada šie dydžiai pridedami kaip vektoriai ir gali būti laikomi tokiais. Dabar galite įvesti kryžminį produktą; apsvarstykite kūną, besisukantį kampiniu greičiu w. Parinkime bet kurį kūno tašką P ir bet kurią koordinačių O pradžią, esančią sukimosi ašyje. Tegu r vektorius, nukreiptas iš O į P. Taškas P juda apskritimu greičiu V = w r sin (w, r). Greičio vektorius V yra apskritimo liestinė ir rodo Fig. aštuoni.

Pažiūrėkime, kaip parašyta kryžminė sandauga pagal komponentus ir vienetų vektorius. Visų pirma, bet kuriam vektoriui A A * A = AA sin 0 = 0.
Todėl vienetinių vektorių atveju i * i = j * j = k * k = 0 ir i * j = k, j * k = i, k * i = j. Tada

Ši lygybė taip pat gali būti parašyta kaip determinantas:

Jei A * B = 0, tai arba A, arba B yra 0, arba A ir B yra kolinijiniai. Taigi, kaip ir taškinės sandaugos atveju, dalijimas iš vektoriaus neįmanomas. Reikšmė A * B yra lygi lygiagretainio, kurio kraštinės A ir B, plotui. Tai lengva pamatyti, nes B sin bA, Bc yra jo aukštis, o A yra pagrindas. Yra daug kitų fizinių dydžių, kurie yra vektoriniai produktai. Vienas iš svarbiausių vektorių sandaugų atsiranda elektromagnetizmo teorijoje ir vadinamas Poitingo vektoriumi P. Šis vektorius pateikiamas taip: P = E * H, kur E ir H yra atitinkamai elektrinio ir magnetinio lauko vektoriai. Vektorius P gali būti laikomas tam tikru energijos srautu vatais kvadratiniam metrui bet kuriame taške. Štai dar keli pavyzdžiai: jėgos momentas F (sukimo momentas) koordinačių, veikiančių tašką, kurio spindulio vektorius r apibrėžtas kaip r * F, pradžios; dalelė, esanti taške r, masė m ir greitis V, turi kampinį momentą mr * V pradžios atžvilgiu; jėga, veikianti dalelę, kuri per magnetinį lauką B greičiu V neša elektros krūvį q, yra qV * B.
Trigubi darbai. Iš trijų vektorių galime sudaryti tris sandaugas: vektorius (A * B) * C; vektorius (A * B) * C; skaliarinis (A * B) * C. Pirmasis tipas yra vektoriaus C ir skaliaro A * B sandauga; apie tokius darbus jau kalbėjome. Antrasis tipas vadinamas dvigubo vektoriaus sandauga; vektorius A * B yra statmenas plokštumai, kurioje yra A ir B, todėl (A * B) * C yra vektorius, esantis plokštumose A ir B ir statmenas C. Todėl apskritai (A * B) * C nėra lygus A * (B * C). Parašydami A, B ir C pagal jų koordinates (komponentus) išilgai x, y ir z ašių ir padaugindami, galite parodyti, kad A * (B * C) = B * (A * C) - C * (A * B). Trečiojo tipo sandauga, atsirandanti skaičiuojant gardelę kietojo kūno fizikoje, skaitine prasme yra lygi gretasienio su briaunomis A, B, C tūriui. Kadangi (A * B) * C = A * (B * C) , skaliarinio ir vektorinio daugybos ženklai gali būti sukeisti, o gabalas dažnai rašomas kaip (ABC). Šis produktas yra lygus determinantui

Atkreipkite dėmesį, kad (A B C) = 0, jei visi trys vektoriai yra toje pačioje plokštumoje arba jei A = 0 arba (ir) B = 0 arba (ir) C = 0.
VEKTORIAUS DIFERENCIACIJA
Tarkime, vektorius U yra vieno skaliarinio kintamojo t funkcija. Pavyzdžiui, U gali būti spindulio vektorius, nubrėžtas nuo pradžios iki judančio taško, o t gali būti laikas. Tegul t pasikeis nedideliu dydžiu Dt, dėl to U pasikeis DU. Tai parodyta pav. 9. Santykis DU / Dt yra vektorius, nukreiptas ta pačia kryptimi kaip ir DU. Galime apibrėžti U išvestinę t as atžvilgiu

jei tokia riba yra. Kita vertus, galite pavaizduoti U kaip komponentų sumą išilgai trijų ašių ir rašyti

Jei U yra spindulio vektorius r, tai dr / dt yra taško greitis, išreikštas laiko funkcija. Vėl diferencijuodami laike, gauname pagreitį. Tarkime, kad taškas juda išilgai kreivės, parodytos Fig. 10. Pažymime s atstumą, kurį taškas nukeliauja išilgai kreivės. Per nedidelį laiko intervalą Dt taškas įveiks atstumą Ds išilgai kreivės; spindulio vektoriaus padėtis pasikeis į Dr. Taigi Dr / Ds yra vektorius, nukreiptas kaip Dr. Toliau

yra kreivės liestinės vieneto vektorius. Tai matyti iš to, kad taškui Q artėjant prie taško P, PQ artėja prie liestinės, o Dr artėja prie Ds. Produkto diferencijavimo formulės yra panašios į skaliarinių funkcijų sandaugos diferencijavimo formules; tačiau kadangi kryžminė sandauga yra antikomutacinė, daugybos tvarka turi būti išsaugota. Štai kodėl,

Taigi matome, kad jei vektorius yra vieno skaliarinio kintamojo funkcija, tai išvestinę galime pavaizduoti taip pat, kaip ir skaliarinės funkcijos atveju.
Vektoriniai ir skaliariniai laukai. Gradientas. Fizikoje dažnai tenka susidurti su vektoriniais arba skaliariniais dydžiais, kurie tam tikroje srityje skiriasi nuo taško iki taško. Tokios teritorijos vadinamos „laukais“. Pavyzdžiui, skaliaras gali būti temperatūra arba slėgis; vektorius gali būti judančio skysčio greitis arba krūvių sistemos elektrostatinis laukas. Jei pasirinkome kokią nors koordinačių sistemą, tai bet kuris taškas P (x, y, z) duotoje srityje atitinka kažkokį spindulio vektorių r (= xi + yj + zk) ir taip pat vektoriaus dydžio reikšmę U (r) arba su juo susietas skaliarinis f (r). Tarkime, kad U ir f yra vienareikšmiškai apibrėžti srityje; tie. kiekvienas taškas atitinka vieną ir tik vieną U arba f reikšmę, nors skirtingi taškai, žinoma, gali turėti skirtingas reikšmes. Tarkime, kad norime apibūdinti greitį, kuriuo U ir f kinta judant šioje srityje. Paprastos dalinės išvestinės, tokios kaip dU / dx ir df / dy, mums netinka, nes jos priklauso nuo konkrečių pasirinktų koordinačių ašių. Tačiau galima įvesti vektorinį diferencialinį operatorių, nepriklausomą nuo koordinačių ašių pasirinkimo; šis operatorius vadinamas "gradientu". Tarkime, kad turime reikalą su skaliariniu lauku f. Pirma, kaip pavyzdį apsvarstykite šalies teritorijos kontūro žemėlapį. Šiuo atveju f yra aukštis virš jūros lygio; kontūrinės linijos jungia taškus, turinčius tą pačią f reikšmę. Judant bet kuria iš šių linijų, f nesikeičia; jei judėsime statmenai šioms tiesėms, tai f kitimo greitis bus didžiausias. Kiekvieną tašką galime susieti su vektoriumi, rodančiu didžiausio greičio f pokyčio dydį ir kryptį; toks žemėlapis ir kai kurie iš šių vektorių parodyti pav. 11. Jei tai padarysime kiekvienam lauko taškui, gausime vektorinį lauką, susietą su skaliariniu lauku f. Tai yra vektoriaus, vadinamo „gradientu“ f, laukas, parašytas grad f arba Cf (simbolis C taip pat vadinamas „nabla“).

kur taškai žymi aukštesnės eilės terminus. Šią išraišką galima parašyti kaip taškinį sandaugą

Dešinę ir kairę šios lygybės puses padalijame iš Ds, o Ds linkę į nulį; tada

kur dr / ds yra vieneto vektorius pasirinkta kryptimi. Išraiška skliausteliuose yra vektorius, priklausantis nuo pasirinkto taško. Taigi, df / ds turi didžiausią reikšmę, kai dr / ds nurodo ta pačia kryptimi, skliausteliuose esanti išraiška yra gradientas. Taigi,

- vektorius, kurio dydis yra lygus ir kryptis sutampa su didžiausiu f pokyčio greičiu koordinačių atžvilgiu. Gradientas f dažnai rašomas kaip

Tai reiškia, kad operatorius C egzistuoja savarankiškai. Daugeliu atvejų jis elgiasi kaip vektorius ir iš tikrųjų yra „vektoriaus diferencialinis operatorius“ – vienas iš svarbiausių fizikos diferencialinių operatorių. Nepaisant to, kad C yra vienetiniai vektoriai i, j ir k, jo fizinė reikšmė nepriklauso nuo pasirinktos koordinačių sistemos. Koks yra ryšys tarp Cf ir f? Visų pirma, tarkime, kad f apibrėžia potencialą bet kuriame taške. Esant bet kokiam nedideliam poslinkiui Dr, f reikšmė pasikeis

Jei q yra dydis (pavyzdžiui, masė, krūvis), perkeltas į Dr, tai darbas, atliktas perkeliant q į Dr, yra lygus

Kadangi Dr - poslinkis, tada qСf - jėga; -Cf – įtempimas (jėga kiekio vienetui), susijusi su f. Pavyzdžiui, tegul U yra elektrostatinis potencialas; tada E yra elektrinio lauko stiprumas, gautas pagal formulę E = -CU. Tarkime, kad U sukuria taškinis elektros krūvis q kulonais, esantis pradinėje vietoje. U reikšmė taške P (x, y, z) su spindulio vektoriumi r pateikiama pagal formulę

Kur e0 yra laisvos erdvės dielektrinė konstanta. Štai kodėl

iš kur išplaukia, kad E veikia r kryptimi ir jo reikšmė yra q / (4pe0r3). Žinodami skaliarinį lauką, galite nustatyti susijusį vektorinį lauką. Galimas ir priešingas. Matematinio apdorojimo požiūriu skaliarinius laukus lengviau valdyti nei vektorinius, nes juos nurodo viena koordinačių funkcija, o vektoriniam laukui reikalingos trys funkcijos, atitinkančios vektoriaus komponentus trimis kryptimis. Taigi kyla klausimas: ar galime užrašyti susijusį skaliarinį lauką, esant vektoriniam laukui?
Divergencija ir rotorius. Matėme C rezultatą, veikiantį skaliarinę funkciją. Kas atsitiks, jei vektoriui taikomas C? Yra dvi galimybės: tegul U (x, y, z) yra vektorius; tada vektorinius ir skaliarinius sandaugus galime sudaryti taip:

Pirmoji iš šių išraiškų yra skaliarė, vadinama divergencija U (žymima divU); antrasis yra vektorius, vadinamas rotoriumi U (žymimas rotU). Šios diferencinės funkcijos, divergencija ir rotorius, yra plačiai naudojamos matematinės fizikos srityse. Įsivaizduokite, kad U yra koks nors vektorius ir kad jis bei pirmieji jo dariniai yra ištisiniai tam tikrame regione. Tegul P yra taškas šioje srityje, apsuptas mažu uždaru paviršiumi S, ribojančiu tūrį DV. Tegul n yra vienetinis vektorius, statmenas šiam paviršiui kiekviename taške (n keičia kryptį judėdamas aplink paviršių, bet visada turi vienetinį ilgį); tegul n nurodo į išorę. Parodykime tai

Čia S nurodo, kad šie integralai paimti per visą paviršių, da yra paviršiaus S elementas. Paprastumo dėlei parinksime patogią formą S mažo gretasienio (kaip parodyta 12 pav.) su kraštinėmis Dx. , Dy ir Dz; taškas P yra gretasienio centras. Iš (4) lygties pirmiausia apskaičiuokime integralą išilgai vieno gretasienio paviršiaus. Priekiniam paviršiui n = i (vieneto vektorius yra lygiagretus x ašiai); Da = DyDz. Indėlis į integralą iš priekinio paviršiaus yra

Priešingoje pusėje n = -i; šis veidas prisideda prie integralo

Naudodami Teiloro teoremą gauname bendrą indėlį iš dviejų veidų

Atminkite, kad DxDyDz = DV. Panašiai galite apskaičiuoti kitų dviejų veidų porų indėlį. Pilnas integralas yra

o jei DV (r) 0, tai aukštesnės eilės terminai išnyksta. Pagal (2) formulę skliausteliuose esanti išraiška yra divU, kuri įrodo (4) lygybę. Lygybę (5) galima įrodyti lygiai taip pat. Vėl panaudokime pav. 12; tada indėlis iš priekinio paviršiaus į integralą bus lygus

Ir naudojant Taylor teoremą, mes nustatome, kad bendras indėlis į integralą iš dviejų veidų turi formą

tie. tai du terminai iš rotU išraiškos (3) lygtyje. Kiti keturi terminai bus gauti atsižvelgus į kitų keturių veidų indėlius. Ką iš esmės reiškia šie santykiai? Apsvarstykite lygybę (4). Tarkime, U yra greitis (pavyzdžiui, skysčio). Tada nЧU da = Un da, kur Un yra normalioji vektoriaus U paviršiaus dedamoji. Todėl Un da ​​yra skysčio, tekančio per da per laiko vienetą, tūris ir skysčio, tekančio per S per laiko vienetą, tūris. Vadinasi,

Tūrio vieneto plėtimosi greitis aplink tašką P. Iš čia divergencija gavo savo pavadinimą; rodomas greitis, kuriuo skystis plečiasi nuo (ty nukrypsta nuo) P. Norėdami paaiškinti fizinę rotoriaus U reikšmę, apsvarstykite kitą paviršiaus integralą per mažą cilindrinį tūrį, kurio aukštis h supa tašką P; plokštumai lygiagretūs paviršiai gali būti orientuoti bet kuria pasirinkta kryptimi. Tegul k yra vieneto vektorius, statmenas kiekvienam paviršiui, ir tegul kiekvieno paviršiaus plotas DA; tada bendras tūris DV = hDA (13 pav.). Dabar apsvarstykite integralą

Taip pat bus pateiktos užduotys savarankiškam sprendimui, į kurias matysite atsakymus.

Vektorinė koncepcija

Prieš išmokdami viską apie vektorius ir operacijas su jais, susitvarkykite su paprastos problemos sprendimu. Yra jūsų verslumo vektorius ir jūsų novatoriškų gebėjimų vektorius. Verslumo vektorius veda į 1 tikslą, o novatoriškų gebėjimų vektorius veda į tikslą 2. Žaidimo taisyklės yra tokios, kad negalite iš karto judėti šių dviejų vektorių kryptimis ir vienu metu pasiekti dviejų tikslų. Vektoriai sąveikauja arba, matematiškai tariant, vektoriais atliekama kokia nors operacija. Šios operacijos rezultatas yra vektorius „Rezultatas“, kuris nukreipia jus į 3 tikslą.

Dabar pasakykite man: kokios operacijos vektoriuose „Įmonė“ ir „Inovatyvūs gebėjimai“ rezultatas yra vektorius „Rezultatas“? Jei negalite pasakyti iš karto, nenusiminkite. Vykdydami šią pamoką galėsite atsakyti į šį klausimą.

Kaip jau matėme aukščiau, vektorius būtinai eina iš tam tikro taško A tiesia linija iki tam tikro taško B... Vadinasi, kiekvienas vektorius turi ne tik skaitinę reikšmę – ilgį, bet ir fizinę bei geometrinę – kryptį. Tai veda prie pirmojo ir paprasčiausio vektoriaus apibrėžimo. Taigi vektorius yra nukreipta atkarpa, einanti iš taško A iki taško B... Jis žymimas taip:.

Ir pradėti kitaip vektorinės operacijos , turime susipažinti su dar vienu vektoriaus apibrėžimu.

Vektorius yra tam tikras taško, į kurį norite patekti iš pradinio taško, atvaizdas. Pavyzdžiui, trimatis vektorius dažniausiai rašomas kaip (x, y, z) . Paprasčiausiai šie skaičiai rodo, kiek reikia nukeliauti trimis skirtingomis kryptimis, kad pasiektumėte tašką.

Tegu pateikiamas vektorius. Kuriame x = 3 (dešinė ranka rodo į dešinę) y = 1 (kairė ranka nukreipta į priekį) z = 5 (po punktu yra laiptai, vedantys į viršų). Pagal šiuos duomenis tašką rasite eidami 3 metrus dešinės rankos nurodyta kryptimi, tada 1 metrą kairiosios rankos nurodyta kryptimi, o tada jūsų lauks laiptai ir užlipę 5 metrus galiausiai pasieksite. atsidurti paskutiniame taške.

Visi kiti terminai yra aukščiau pateikto paaiškinimo patikslinimai, būtini atliekant įvairias operacijas su vektoriais, tai yra sprendžiant praktines problemas. Peržiūrėkime šiuos griežtesnius apibrėžimus, apsistodami ties tipiškomis vektorių problemomis.

Fiziniai pavyzdžiai vektoriniai dydžiai gali būti erdvėje judančio materialaus taško poslinkis, šio taško greitis ir pagreitis, taip pat jį veikianti jėga.

Geometrinis vektorius pateikta dvimatėje ir trimatėje erdvėje formoje kryptinis segmentas... Tai segmentas, skiriantis pradžią ir pabaigą.

Jeigu A yra vektoriaus pradžia ir B- jo pabaiga, tada vektorius žymimas simboliu arba viena mažąja raide. Paveiksle vektoriaus pabaiga pažymėta rodykle (1 pav.)

Ilgis(arba modulis) geometrinio vektoriaus atkarpos ilgis

Du vektoriai vadinami lygus jei jas galima išlyginti (jei kryptys sutampa) lygiagrečiojo perkėlimo būdu, t.y. jei jie lygiagretūs, nukreipti ta pačia kryptimi ir vienodo ilgio.

Fizikoje dažnai manoma inkaruoti vektoriai nurodytas pagal taikymo vietą, ilgį ir kryptį. Jei vektoriaus taikymo taškas nesvarbus, tada jį galima perkelti išlaikant ilgį ir kryptį į bet kurį erdvės tašką. Šiuo atveju vektorius vadinamas Laisvas... Sutiksime tik svarstyti laisvi vektoriai.

Tiesinės operacijos geometriniais vektoriais

Vektoriaus padauginimas iš skaičiaus

Vektoriaus sandauga pagal skaičių vadinamas vektoriumi, gautu iš vektoriaus išplečiant (at) arba suspaudžiant (at) kartus, o vektoriaus kryptis išsaugoma jei, ir pasikeičia į priešingą, jei. (2 pav.)

Iš apibrėžimo matyti, kad vektoriai ir = visada yra vienoje arba lygiagrečiose tiesėse. Tokie vektoriai vadinami kolinearinis... (Taip pat galite sakyti, kad šie vektoriai yra lygiagretūs, bet vektoriaus algebroje įprasta sakyti "kolinearinis".) Taip pat yra priešingai: jei vektoriai ir yra kolineariniai, tai jie yra susiję ryšiu.

Todėl lygybė (1) išreiškia dviejų vektorių kolineariškumo sąlygą.

Vektorių sudėjimas ir atėmimas

Pridėdami vektorius, turite tai žinoti suma vektoriais ir vadinamas vektoriumi, kurio pradžia sutampa su vektoriaus pradžia, o pabaiga – su vektoriaus pabaiga, jeigu vektoriaus pradžia yra prijungta prie vektoriaus galo. (3 pav.)

Šis apibrėžimas gali būti paskirstytas bet kokiam baigtiniam vektorių skaičiui. Tegul suteikiama erdvė n laisvi vektoriai. Sudėjus kelis vektorius, jų suma imamas uždaromasis vektorius, kurio pradžia sutampa su pirmojo vektoriaus pradžia, o pabaiga - su paskutinio vektoriaus pabaiga. Tai yra, jei prijungiate vektoriaus pradžią prie vektoriaus pabaigos, o vektoriaus pradžią - prie vektoriaus pabaigos ir pan. ir galiausiai iki vektoriaus pabaigos - vektoriaus pradžios, tada šių vektorių suma yra uždarymo vektorius kurio pradžia sutampa su pirmojo vektoriaus pradžia, o pabaiga – su paskutinio vektoriaus pabaiga. (4 pav.)

Terminai vadinami vektoriaus komponentais, o suformuluota taisyklė yra daugiakampio taisyklė... Šis daugiakampis negali būti plokščias.

Padauginę vektorių iš -1, gausite priešingą vektorių. Vektoriai ir turi tą patį ilgį ir priešingas kryptis. Jų suma duoda nulinis vektorius kurio ilgis lygus nuliui. Nulinio vektoriaus kryptis neapibrėžta.

Vektorinėje algebroje nereikia atskirai svarstyti atimties operacijos: vektoriaus atėmimas iš vektoriaus reiškia prie vektoriaus pridėti priešingą vektorių, t.y.

1 pavyzdys. Supaprastinkite išraišką:

.

,

tai yra, vektorius galima sudėti ir padauginti iš skaičių taip pat, kaip ir daugianario (ypač taip pat ir reiškinių supaprastinimo užduotys). Paprastai poreikis supaprastinti tiesiškai panašias išraiškas vektoriais iškyla prieš skaičiuojant vektorių sandaugas.

2 pavyzdys. Vektoriai ir tarnauja kaip lygiagretainio ABCD įstrižainės (4a pav.). Išreikškite abiem vektoriais ir, kurie yra šio lygiagretainio kraštinės.

Sprendimas. Lygiagretainio įstrižainių susikirtimo taškas kiekvieną įstrižainę dalija pusiau. Problemos teiginyje reikalingų vektorių ilgius randame kaip pusę vektorių sumų, sudarančių trikampį su norimais, arba kaip pusę skirtumų (priklausomai nuo vektoriaus, kuris tarnauja kaip įstrižainė, krypties), arba kaip pastaruoju atveju pusė sumos, paimtos su minuso ženklu. Rezultatas yra vektoriai, kurių reikia problemos teiginyje:

Yra pagrindo manyti, kad dabar teisingai atsakėte į klausimą apie verslumo ir naujoviškų gebėjimų vektorius šios pamokos pradžioje. Teisingas atsakymas: su šiais vektoriais atliekama sudėjimo operacija.

Pats išspręskite vektorines problemas ir tada pamatykite sprendimus

Kaip rasti vektorių sumos ilgį?

Ši užduotis užima ypatingą vietą vektorinėse operacijose, nes ji apima trigonometrinių savybių naudojimą. Tarkime, kad susiduriate su tokia užduotimi, kaip ši:

Atsižvelgiant į vektorių ilgius ir šių vektorių sumos ilgis. Raskite šių vektorių skirtumo ilgį.

Šios ir kitų panašių problemų sprendimai bei paaiškinimai, kaip jas išspręsti – pamokoje “ Vektoriaus pridėjimas: vektorių sumos ilgis ir kosinuso teorema ".

Ir jūs galite patikrinti tokių problemų sprendimą Internetinis skaičiuotuvas "Nežinoma trikampio kraštinė (vektoriaus sudėjimas ir kosinuso teorema)" .

Kur yra vektorių sandaugos?

Vektoriaus sandaugos iš vektoriaus nėra tiesinės operacijos ir nagrinėjamos atskirai. Ir mes turime pamokas „Vektoriaus taškinė sandauga“ ir „Vektorių ir mišri vektorių sandauga“.

Vektoriaus projekcija į ašį

Vektoriaus projekcija į ašį yra lygi projektuojamo vektoriaus ilgio sandaugai iš kampo tarp vektoriaus ir ašies kosinuso:

Kaip žinote, taško projekcija A tiesėje (plokštumoje) yra statmeno, nuleisto iš šio taško tiesėje (plokštumoje), pagrindas.

Leisti būti savavališkas vektorius (5 pav.), ir būti jo pradžios projekcijos (taškai A) ir pabaiga (taškai B) vienai ašiai l... (Norėdami sukurti taško projekciją A) tiesia linija per tašką A plokštuma, statmena tiesei. Tiesės ir plokštumos sankirta apibrėžia reikiamą projekciją.

Vektorinis komponentas l ašyje vadinamas ant šios ašies gulinčiu vektoriumi, kurio pradžia sutampa su pradžios projekcija, o pabaiga – su vektoriaus pabaigos projekcija.

Vektoriaus projekcija į ašį l paskambino numeriu

,

lygus komponento vektoriaus ilgiui šioje ašyje, paimtam su pliuso ženklu, jei komponento kryptis sutampa su ašies kryptimi l, ir su minuso ženklu, jei šios kryptys yra priešingos.

Pagrindinės vektorinių projekcijų ašyje savybės:

1. Lygių vektorių projekcijos į tą pačią ašį yra lygios viena kitai.

2. Dauginant vektorių iš skaičiaus, jo projekcija dauginama iš to paties skaičiaus.

3. Vektorių sumos projekcija bet kurioje ašyje yra lygi projekcijų sumai toje pačioje vektorių sumos ašyje.

4. Vektoriaus projekcija į ašį lygi projektuojamo vektoriaus ilgio sandaugai kampo tarp vektoriaus ir ašies kosinuso:

.

Sprendimas. Projektuoti vektorius į ašį l kaip apibrėžta aukščiau esančiame teoriniame pagrinde. Iš 5a pav. akivaizdu, kad vektorių sumos projekcija yra lygi vektorių projekcijų sumai. Mes apskaičiuojame šias prognozes:

Raskite galutinę vektorių sumos projekciją:

Vektoriaus ryšys su stačiakampe Dekarto koordinačių sistema erdvėje

Pažintis su atitinkamoje pamokoje vyko stačiakampė Dekarto koordinačių sistema erdvėje, pageidautina jį atidaryti naujame lange.

Sutvarkytoje koordinačių sistemoje 0xyz ašį Jautis paskambino abscisė, ašis 0 m – y ašis, ir ašis 0z – ašis taikyti.

Su savavališku tašku M erdvė, kurią susiejame su vektoriumi

paskambino spindulio vektorius taškų M ir suprojektuokite jį į kiekvieną koordinačių ašį. Pažymime atitinkamų projekcijų reikšmes:

Numeriai x, y, z yra vadinami taško M koordinatės, atitinkamai abscisė, ordinatės ir kreiptis, ir yra parašyti kaip tvarkingas skaičių taškas: M (x; y; z)(6 pav.).

Vadinamas vienetinio ilgio vektorius, kurio kryptis sutampa su ašies kryptimi vieneto vektorius(arba ortomas) ašis. Pažymėkime pagal

Atitinkamai koordinačių ašių vienetiniai vektoriai Jautis, Oy, Ozas

Teorema. Bet kurį vektorių galima išplėsti išilgai koordinačių ašių vienetų vektorių:

(2)

Lygybė (2) vadinama vektoriaus išplėtimu išilgai koordinačių ašių. Šio plėtimosi koeficientai yra vektoriaus projekcijos į koordinačių ašis. Taigi, vektoriaus plėtimosi koeficientai (2) išilgai koordinačių ašių yra vektoriaus koordinatės.

Pasirinkus tam tikrą koordinačių sistemą erdvėje, vektorius ir jos koordinačių tripletas viena kitą viena kitą lemia, todėl vektorius gali būti parašytas forma

Vektoriaus atvaizdavimas formomis (2) ir (3) yra identiškas.

Kolineariškumo sąlyga vektoriams koordinatėse

Kaip jau minėjome, vektoriai vadinami kolineariniais, jei jie yra susiję ryšiu

Tegul vektoriai ... Šie vektoriai yra kolineariniai, jei vektorių koordinatės yra susietos ryšiu

,

tai vektorių koordinatės yra proporcingos.

6 pavyzdys. Duoti vektoriai ... Ar šie vektoriai yra kolineariniai?

Sprendimas. Išsiaiškinkime šių vektorių koordinačių santykį:

.

Vektorių koordinatės yra proporcingos, todėl vektoriai yra kolineariniai arba lygiagretūs.

Vektoriaus ilgio ir krypties kosinusai

Dėl koordinačių ašių tarpusavio statmenumo vektoriaus ilgis

yra lygus stačiakampio gretasienio, pastatyto ant vektorių, įstrižainės ilgiui

ir išreiškiamas lygybe

(4)

Vektorius yra visiškai apibrėžtas nurodant du taškus (pradžios ir pabaigos), todėl vektoriaus koordinates galima išreikšti šių taškų koordinatėmis.

Tegu nurodytoje koordinačių sistemoje vektoriaus pradžia yra taške

ir pabaiga yra taške

Iš lygybės

Tai seka

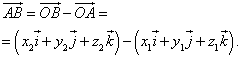
arba koordinačių forma

Vadinasi, vektoriaus koordinatės lygios vektoriaus pabaigos ir pradžios to paties pavadinimo koordinačių skirtumams ... Formulė (4) šiuo atveju įgauna formą

Vektoriaus kryptis nustatoma pagal krypties kosinusai ... Tai kampų, kuriuos vektorius sudaro su ašimis, kosinusai Jautis, Oy ir Ozas... Pažymėkime atitinkamai šiuos kampus α , β ir γ ... Tada šių kampų kosinusus galima rasti pagal formules

Kryptiniai vektoriaus kosinusai taip pat yra šio vektoriaus vienetinio vektoriaus koordinatės, taigi ir vektoriaus vektoriaus

.

Atsižvelgiant į tai, kad vektoriaus vieneto ilgis yra lygus vienam vienetui, tai yra

,

gauname tokią lygybę krypties kosinusams:

7 pavyzdys. Raskite vektoriaus ilgį x = (3; 0; 4).

Sprendimas. Vektoriaus ilgis yra

8 pavyzdys. Taškai skiriami:

Išsiaiškinkite, ar iš šių taškų pastatytas trikampis yra lygiašonis.

Sprendimas. Naudodami vektoriaus ilgio formulę (6), randame kraštinių ilgius ir nustatome, ar tarp jų yra dvi vienodos:

Rastos dvi lygios kraštinės, todėl trečiosios kraštinės ilgio ieškoti nereikia, o duotasis trikampis yra lygiašonis.

9 pavyzdys. Raskite vektoriaus ilgį ir jo krypties kosinusus, jei .

Sprendimas. Pateikiamos vektorinės koordinatės:

.

Vektoriaus ilgis lygus kvadratinei šaknims iš vektoriaus koordinačių kvadratų sumos:

.

Raskite krypties kosinusus:

Išspręskite vektoriaus uždavinį patys ir tada pamatykite sprendimą

Veiksmai su vektoriais, nurodytais koordinačių forma

Duokime du vektorius ir pagal jų projekcijas:

Nurodykime veiksmus su šiais vektoriais.

APIBRĖŽIMAS

Vektorius(iš lat. vektorius"-" guolis ") - nukreiptas tiesios linijos segmentas erdvėje arba plokštumoje.

Grafiškai vektorius vaizduojamas kaip tam tikro ilgio nukreipta linijos atkarpa. Vektorius, kurio pradžia yra taške, o pabaiga – taške, žymimas kaip (1 pav.). Be to, vektorius gali būti pažymėtas viena maža raide, pavyzdžiui,.

Jei koordinačių sistema nurodyta erdvėje, tai vektorius gali būti vienareikšmiškai nurodytas jo koordinačių aibe. Tai reiškia, kad vektorius suprantamas kaip objektas, turintis dydį (ilgį), kryptį ir taikymo tašką (vektoriaus pradžią).

Vektorinio skaičiavimo užuomazgos darbuose pasirodė 1831 metais vokiečių matematiko, mechaniko, fiziko, astronomo ir geodezisto Johano Karlo Friedricho Gauso (1777-1855) darbuose. Darbus apie operacijas su vektoriais paskelbė airių matematikas, mechanikas ir teorinis fizikas seras Williamas Rowanas Hamiltonas (1805–1865) kaip savo ketvirčio skaičiavimo dalį. Mokslininkas pasiūlė terminą „vektorius“ ir aprašė kai kurias operacijas su vektoriais. Vektoriniai skaičiavimai buvo toliau plėtojami britų fiziko, matematiko ir mechaniko Jameso Clerko Maxwello (1831–1879) dėka elektromagnetizmo darbų. 1880-aisiais buvo išleista amerikiečių fiziko, fizikochemiko, matematiko ir mechaniko Josiah Willard Gibbs (1839–1903) knyga „Vektorinės analizės elementai“. Šiuolaikinę vektorinę analizę 1903 metais aprašė anglų savamokslis mokslininkas, inžinierius, matematikas ir fizikas Oliveris Heaviside'as (1850-1925).

APIBRĖŽIMAS

Ilgis arba vektorinis modulis yra nukreiptos atkarpos, kuri apibrėžia vektorių, ilgis. Jis nurodomas kaip.

Pagrindiniai vektorių tipai

Nulinis vektorius yra vektorius, kurio pradžios ir pabaigos taškai sutampa. Nulinio vektoriaus ilgis lygus nuliui.

Vadinami vektoriai, lygiagretūs vienai tiesei arba gulintys vienoje tiesėje kolinearinis(2 pav.).

bendrai režisavo jei jų kryptys sutampa.

2 paveiksle tai vektoriai ir. Vektorių kryptingumas žymimas taip:.

Vadinami du kolineariniai vektoriai nukreipta priešingai jei jų kryptys yra priešingos.

3 paveiksle tai vektoriai ir. Pavadinimas:.